题目内容
周长为定值a的扇形,这个扇形的半径R的范围是
- A.

- B.
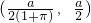
- C.(a,2a)
- D.(0,a)
B
分析:设圆心角为m,根据弧长公式求出弧长,然后用含a和R的式子表示出圆心角m,再根据圆心角的范围可得出R的范围.
解答:设圆心角为m,则a=2R+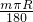 =(2+
=(2+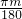 )R
)R
∴R= ,
,
又∵0<m<360,
∴0<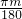 <2π,
<2π,
∴2<2+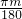 <2π+2,
<2π+2,
∴ <R<
<R< .
.
故选B.
点评:此题考查了弧长的计算,解答本题的关键是设出圆心角,然后表示出圆心角的范围,继而得出半径的范围,有一定的难度,注意熟练掌握弧长公式.
分析:设圆心角为m,根据弧长公式求出弧长,然后用含a和R的式子表示出圆心角m,再根据圆心角的范围可得出R的范围.
解答:设圆心角为m,则a=2R+
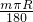 =(2+
=(2+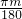 )R
)R∴R=
 ,
,又∵0<m<360,
∴0<
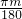 <2π,
<2π,∴2<2+
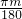 <2π+2,
<2π+2,∴
 <R<
<R< .
.故选B.
点评:此题考查了弧长的计算,解答本题的关键是设出圆心角,然后表示出圆心角的范围,继而得出半径的范围,有一定的难度,注意熟练掌握弧长公式.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
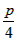 时扇形的面积最大 |
时扇形的面积最大 |