Question

【题目】如图，AD∥BC，∠BAD＝90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连结BE，过C点作CF⊥BE，垂足为F．

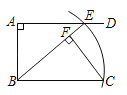
（1）线段BF与图中现有的哪一条线段相等？先将你猜想出的结论填写在下面的横线上，然后再加以证明．

结论：BF＝　 　；

（2）若AB＝6，AE＝8，求点A到点C的距离．

Answer 1

【答案】（1）AE，证明见解析；（2）AC＝2.

【解析】

（1）由已知得BF=AE；由AD与BC平行得到一对内错角相等，再由一对直角相等，且BE=CB，利用AAS得到△AEB≌△FBC，利用全等三角形对应角相等即可得证．
（2）连接AC，如图所示，由（1）的全等三角形得到对应边相等，进而求出BE与BC的长，则AC的长可求出．

（1）BF＝AE，

故答案为：AE；

证明：∵CF⊥BE，

∴∠A＝∠BFC＝90°，

∵AD∥BC，

∴∠AEB＝∠FBC，

在△AEB和△FBC中，

，

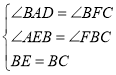∴△AEB≌△FBC（AAS），

∴BF＝AE．

（2）连接AC，如图所示，

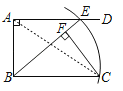
∵△AEB≌△FBC，

∴∠CBF＝∠AEB，BE＝BC，

∵∠ABE+∠AEB＝90°，

∴∠ABE+∠CBF＝90°，

即∠ABC＝90°，

又AB＝6，AE＝8，

∴，

∴BE＝BC＝10，

∴．