题目内容
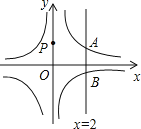
【题目】如图,直线x=2与反比例函数![]() 和
和![]() 的图象分别交于A、B两点.若点P是y轴上任意一点,△PAB的面积是3,则k=______.
的图象分别交于A、B两点.若点P是y轴上任意一点,△PAB的面积是3,则k=______.
【答案】4
【解析】
如图,连接OA、OB.设x=2与x轴交于点C.因为△OAB与△PAB是等底同高的两个三角形,所以它们的面积相等,即△OAB的面积是3.所以由反比例函数系数k的几何意义知△OAB的面积=![]() ×2+
×2+![]() |-k|=3,由此易求k的值.
|-k|=3,由此易求k的值.
如图,

∵点P是y轴上任意一点,直线x=2与反比例函数![]() 和
和![]() 的图象分别交于A、B两点(即AB∥y轴),
的图象分别交于A、B两点(即AB∥y轴),
∴S△OAB=S△PAB=3,
又∵点A、B分别是反比例函数![]() 和
和![]() 的图象上的点,
的图象上的点,
∴S△OAB=S△OAC+S△OBC=![]() ×2+
×2+![]() |-k|=3,
|-k|=3,
解得,k=4或k=-4(不合题意,舍去).
故答案是:4.

练习册系列答案
相关题目