题目内容
【题目】在某张三角形纸片上，取其一边的中点，沿着过这点的两条中位线分别剪去两个三角形，剩下的部分就是如图所示的四边形；经测量这个四边形的相邻两边长为10cm，6cm，一条对角线的长为8cm；则原三角形纸片的周长是_______．
【答案】48cm或(32＋8
)cm
【解析】分析: 首先补全三角形进而利用平行四边形的性质得出各边长进而得出答案,解答本题应分两种情况进行．
详解: 如图1：
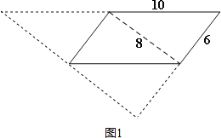
周长为：2×（10+8+6）=48（cm）；
如图2：
∵BD=6，BC=8，CD=10，
∴BD2+BC2=CD2，
∴△BCD是直角三角形，
∴∴ACB=∠CBD=90°,
在Rt△ABC中，由勾股定理得，
AB=
，
∴周长为2×(10+4+6)=(32+8)（cm）；
综上所述：原三角形纸片的周长是48或(32+8)cm．
故答案为：48或（32+8）cm．
练习册系列答案
相关题目
