题目内容
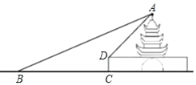
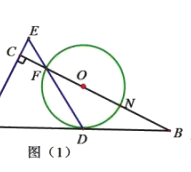
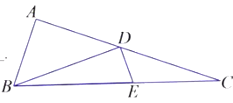
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 分别在
分别在![]() 边上,
边上,![]() ,且
,且![]() ,若
,若![]() ,则
,则![]() 的长是__________.
的长是__________.
【答案】![]()
【解析】
根据已知条件和等腰三角形的性质可先求得∠BDE=90°,然后根据三角形相似的判定和性质可得![]() ,从而可得AD+DC=3AB,然后再利用勾股定理求得CD,从而可得AC和AB,再利用勾股定理求得BC即可.
,从而可得AD+DC=3AB,然后再利用勾股定理求得CD,从而可得AC和AB,再利用勾股定理求得BC即可.
解:∵∠C+![]() ∠CDE=45°,
∠CDE=45°,
∴ ∠CDE+2∠C=90°,
又∵ BD=CD,
∴∠DBE=∠C,
∴∠C+∠DBE+∠CDE=90°,
∴∠BDE=90°,
又∵∠A=90°,
∴△BDE∽△CAB,
∴![]() ,
,
∵AC=AD+DC,
∴AD+DC=3AB,
又∵AB2+AD2=BD2=CD2,
∴![]() ,解得CD=
,解得CD=![]() (CD=-6舍),
(CD=-6舍),
∴AC=![]() ,AB=
,AB=![]() ,
,
∴BC=![]() .
.

练习册系列答案
相关题目