题目内容
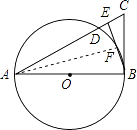
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC= ![]() ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F. 
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC= ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:连接AF.
∵AB为直径,
∴∠AFB=90°.
∵AE=AB,
∴△ABE为等腰三角形.
∴∠BAF= ![]() ∠BAC.
∠BAC.
∵∠EBC= ![]() ∠BAC,
∠BAC,
∴∠BAF=∠EBC,
∴∠FAB+∠FBA=∠EBC+∠FBA=90°.
∴∠ABC=90°.
即AB⊥BC,
∴BC与⊙O相切
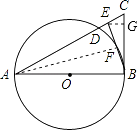
(2)解:过E作EG⊥BC于点G,
∵∠BAF=∠EBC,
∴sin∠BAF=sin∠EBC= ![]() .
.
在△AFB中,∠AFB=90°,
∵AB=8,
∴BF=ABsin∠BAF=8× ![]() =2,
=2,
∴BE=2BF=4.
在△EGB中,∠EGB=90°,
∴EG=BEsin∠EBC=4× ![]() =1,
=1,
∵EG⊥BC,AB⊥BC,
∴EG∥AB,
∴△CEG∽△CAB,
∴ ![]() .
.
∴ ![]() ,
,
∴CE= ![]() ,
,
∴AC=AE+CE=8+ ![]() =
= ![]() .
.
【解析】(1)首先连接AF,由AB为直径,根据圆周角定理,可得∠AFB=90°,又由AE=AB,∠EBC= ![]() ∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.
∠BAC,根据等腰三角形的性质,可得∠BAF=∠EBC,继而证得BC与⊙O相切;(2)首先过E作EG⊥BC于点G,由三角函数的性质,可求得BF的长,易证得△CEG∽△CAB,然后由相似三角形的对应边成比例,求得答案.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目