Question

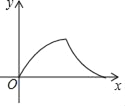
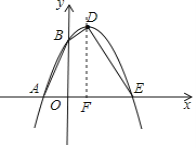
【题目】如图，已知抛物线与x轴交于点A（﹣1，0），E（3，0）两点,与y轴交于点B（0，3）．

（1）求抛物线的解析式；

（2）设抛物线的顶点为D，求四边形AEDB的面积．

Answer 1

【答案】（1）y＝﹣x2+2x+3；（2）9

【解析】

（1）设交点式函数解析式y＝a（x+1）（x﹣3），将点B的坐标代入即可得到答案.

（2）根据顶点坐标的公式求出点D的坐标，对称轴与x轴的交点F，利用DF将四边形分割为三部分图形面积相加即可解答.

（1）∵抛物线与x轴相交于点A（﹣1，0），E（3，0），故设抛物线的解析式为y＝a（x+1）（x﹣3）．

∵抛物线与y轴相交于点B（0，3），

∴a（0+1）（0﹣3）＝3，

∴a＝﹣1．

∴抛物线的解析式为y＝﹣（x+1）（x﹣3），

即y＝﹣x2+2x+3；

（2）如题图，设对称轴与x轴相交于F，

∵

∴点D的坐标为（1，4），

∴点F的坐标为（1，0）．

∴S四边形AEDB＝S△OAB+S四边形DBOF+S△DEF＝OAOB+（OB+DF）OF+EFDF＝×1×3+×（3+4）×1+×2×4＝9．