Question

【题目】如图，在四边形ABCD中，BC＞BA，AD=DC，

（1）若BD⊥CD，∠C=60°，BC=10，求AD的长；

（2）若BD平分∠ABC，求证：∠A+∠C=180°。

Answer 1

【答案】（1）AD=5；（2）证明见解析；

【解析】

(1)由“在直角三角形中， 30°所对的直角边是斜边的一半”可得，CD=BC=5，再由AD=DC，可求出AD的长.

（2）先在线段BC上截取BE=BA,连接DE,根据BD平分∠ABC,可得∠ABD=∠EBD,

根据,可判定△ABD≌△EBD,根据全等三角形的性质可得:AD=ED,∠A=∠BED．再根据AD=CD,等量代换可得ED=CD,根据等边对等角可得:∠DEC=∠C．

由∠BED+∠DEC=180°,可得∠A+∠C=180°．

（1）∵BD⊥CD，

∴∠BDC=90°，

∵∠C=60°，

∴∠DBC=30°，

又BC=10，

∴CD=BC=5，

即AD=DC=5.

（2）证明:在线段BC上截取BE=BA,连接DE,如图所示,

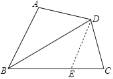
∵BD平分∠ABC，

∴∠ABD=∠EBD，

在△ABD和△EBD中，

，

∴△ABD≌△EBD（SAS），

∴AD=ED,∠A=∠BED．

∵AD=CD，

∴ED=CD，

∴∠DEC=∠C．

∵∠BED+∠DEC=180°，

∴∠A+∠C=180°．