题目内容
【题目】如图,直线![]() 交
交![]() 轴于点A,交
轴于点A,交![]() 轴于点B,抛物线
轴于点B,抛物线![]() 经过点A,交
经过点A,交![]() 轴于点
轴于点![]() ,点P为直线AB下方抛物线上一动点,过点P作
,点P为直线AB下方抛物线上一动点,过点P作![]() 于D,连接AP.
于D,连接AP.
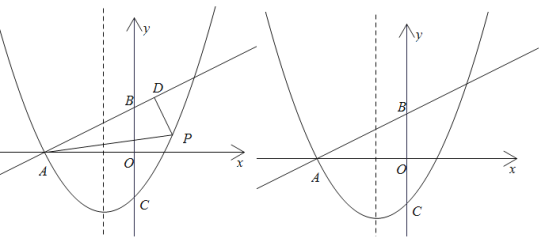
(1)求抛物线的解析式;
(2)若以点![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点P的坐标;
相似,求点P的坐标;
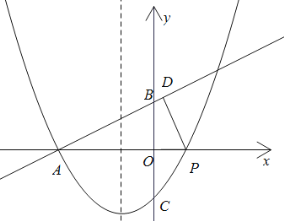
(3)将![]() 绕点A旋转,当点O的对应点
绕点A旋转,当点O的对应点![]() 落在抛物线的对称轴上时,请直接写出点B的对应点
落在抛物线的对称轴上时,请直接写出点B的对应点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时三角形相似;(3)点
时三角形相似;(3)点![]() 的坐标为
的坐标为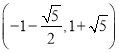 或
或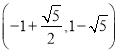 .
.
【解析】
(1)先求出A,B的坐标,然后根据抛物线![]() 经过点A,C,解出a,c的值,即可求出抛物线解析式;
经过点A,C,解出a,c的值,即可求出抛物线解析式;
(2)分①当![]() 时和②当
时和②当![]() 时两种情况讨论即可;
时两种情况讨论即可;
(3)先将抛物线的解析式化为顶点式,得出抛物线的对称轴为:x=-1,根据![]() ,得出AO=3,BO=
,得出AO=3,BO=![]() ,然后设O
,然后设O![]() (-1,m),解出m值,分①当O
(-1,m),解出m值,分①当O![]() (-1,
(-1,![]() )时和②当O
)时和②当O![]() (-1,-
(-1,-![]() )时两种情况讨论即可.
)时两种情况讨论即可.
(1)∵直线![]() 交
交![]() 轴于A,B,
轴于A,B,
![]() ,
,
∵抛物线![]() 经过点A,C,
经过点A,C,
∴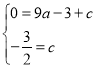 ,
,
解得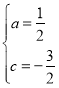 ,
,
∴抛物线解析式为![]() ;
;
(2)①当![]() 时,点P为抛物线与x轴的交点,
时,点P为抛物线与x轴的交点,
令![]() ,
,
解得![]() (舍去)
(舍去)
∴点P的坐标为![]() ;
;
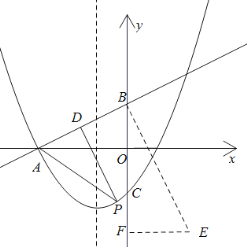
②当![]() 时,
时,![]() ,
,
![]() ,
,
过点B作![]() ,且使得
,且使得![]() ,则P点必在直线AE与抛物线的交点上,
,则P点必在直线AE与抛物线的交点上,
做![]() 轴于点F,
轴于点F,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设直线AE的解析式为![]()
则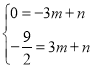 ,
,
解得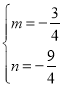 ,
,
∴直线AE的解析式为![]() ,
,
解方程组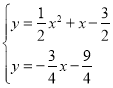
解得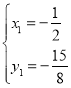 ,
,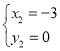 ,
,
∴点P的坐标为![]() ,
,
∴当![]() 或(1,0)时三角形相似;
或(1,0)时三角形相似;
(3)由题抛物线的解析式为![]() ,
,
∴抛物线的对称轴为:x=-1,
∵![]() ,
,
∴AO=3,BO=![]() ,
,
∴设O![]() (-1,m),
(-1,m),
则有AO![]() =
=![]() =AO=3,
=AO=3,
解得:m=![]() 或m=
或m=![]() ,
,
①当O![]() (-1,
(-1,![]() )时,
)时,
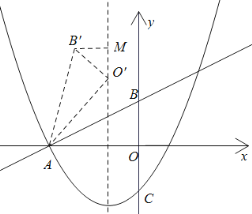
设AO![]() 的解析式为:y=ax+b,
的解析式为:y=ax+b,
将A(-3,0),O![]() (-1,
(-1,![]() )代入得
)代入得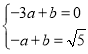 ,
,
解得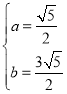 ,
,
∴AO![]() 的解析式为:y=
的解析式为:y=![]() x+
x+![]() ,
,
∵B![]() O
O![]() ⊥AO
⊥AO![]() ,
,
∴可设B![]() O
O![]() 的解析式为:y=
的解析式为:y=![]() x+b1,
x+b1,
将O![]() (-1,
(-1,![]() )代入得
)代入得![]() =
=![]() ×(-1)+b1,
×(-1)+b1,
解得b1=![]() ,
,
∴B![]() O
O![]() 的解析式为:y=
的解析式为:y=![]() x+
x+![]() ,
,
设B![]() 的坐标为(x,
的坐标为(x,![]() x+
x+![]() ),
),
则B![]() O
O![]() =
=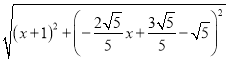 =BO=
=BO=![]() ,
,
解得x1=-1-![]() ,x2=-1-
,x2=-1-![]() (不符合此时的情况,舍去),
(不符合此时的情况,舍去),
将x1代入![]() x+
x+![]() =1+
=1+![]() ,
,
∴B![]() 的坐标为(-1-
的坐标为(-1-![]() ,1+
,1+![]() );
);
②当O![]() (-1,-
(-1,-![]() )时,
)时,
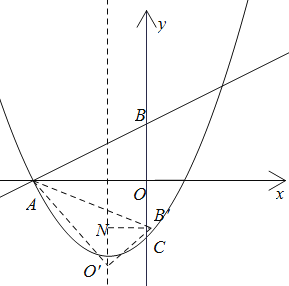
同理可得B![]() 的坐标为(-1+
的坐标为(-1+![]() ,1-
,1-![]() );
);
综上:点![]() 的坐标为
的坐标为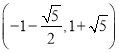 或
或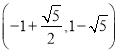 .
.

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案