题目内容
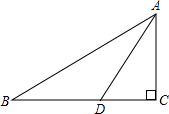
如图所示,在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC交BC于E,交CD于F,FG∥AB交BC于G.试判断CE,CF,GB的数量关系,并说明理由.
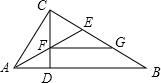

CE=CF=GB.
理由如下:
(1)∵∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵CD⊥AB,
∴∠ACD+∠CAD=90°.
∴∠ACD=∠ABC.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∵∠CEF=∠BAE+∠ABC,∠CFE=∠CAE+∠ACD,
∴∠CEF=∠CFE.
∴CE=CF(等角对等边).
(2)如图,过E作EH⊥AB于H,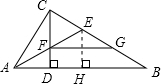
∵AE平分∠BAC,EH⊥AB,EC⊥AC,
∴EH=EC(角平分线上的点到角两边的距离相等).
∴EH=CF.
∵FG∥AB,
∴∠CGF=∠EBH.
∵CD⊥AB,EH⊥AB,
∴∠CFG=∠EHB=90°.
在Rt△CFG和Rt△EHB中
∵∠CGF=∠EBH,∠CFG=∠EHB,CF=EH,
∴Rt△CFG≌Rt△EHB.
∴CG=EB.
∴CE=GB.
∴CE=CF=GB.
理由如下:
(1)∵∠ACB=90°,
∴∠BAC+∠ABC=90°.
∵CD⊥AB,
∴∠ACD+∠CAD=90°.
∴∠ACD=∠ABC.
∵AE平分∠BAC,
∴∠BAE=∠CAE.
∵∠CEF=∠BAE+∠ABC,∠CFE=∠CAE+∠ACD,
∴∠CEF=∠CFE.
∴CE=CF(等角对等边).
(2)如图,过E作EH⊥AB于H,

∵AE平分∠BAC,EH⊥AB,EC⊥AC,
∴EH=EC(角平分线上的点到角两边的距离相等).
∴EH=CF.
∵FG∥AB,
∴∠CGF=∠EBH.
∵CD⊥AB,EH⊥AB,
∴∠CFG=∠EHB=90°.
在Rt△CFG和Rt△EHB中
∵∠CGF=∠EBH,∠CFG=∠EHB,CF=EH,
∴Rt△CFG≌Rt△EHB.
∴CG=EB.
∴CE=GB.
∴CE=CF=GB.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目