Question

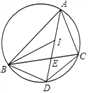
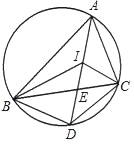
【题目】如图，I是△ABC的内心，AI的延长线与△ABC的外接圆相交于点D，与BC交于点E，连接BI、CI、BD、DC．下列说法中正确的有（　　）

①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合；

②I到△ABC三个顶点的距离相等；③∠BIC=90°+∠BAC；

④线段DI是线段DE与DA的比例中项；⑤点D是△BIC的外心．

A. 1个 B. 2个 C. 3个 D. 4个

Answer 1

【答案】D

【解析】试题解析：①∵I是△ABC的内心，

∴AI平分∠BAC，

∴∠CAD=∠DAB，

∴∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合；

所以此选项说法正确；

②∵I是△ABC的内心，

∴I是△ABC三个角平分线的交点，

∴I到△ABC三边的距离相等，

所以此选项说法不正确；

③∵I是内心，

∴BI、CI分别平分∠ABC、∠ACB，

∴∠ABI=∠ABC，∠ACI=∠ACB，

∵∠BIE=∠ABI+∠BAI，∠EIC=∠DAC+∠ACI，

∴∠BIC=∠BIE+∠EIC=∠ABI+∠BAI+∠DAC+∠ACI，

∵∠ABC+∠ACB=180°﹣∠BAC，

∴∠ABC+∠ACB=90°﹣∠BAC，

∴∠ABI+∠ACI=90°﹣∠BAC，

∴∠BIC=90°﹣∠BAC+∠BAC=90°+∠BAC，

所以此选项说法正确；

④∵∠DCB=∠BAD，∠BAD=∠DAC，

∴∠DCB=∠DAC，

∵∠ADC=∠ADC，

∴△ADC∽△CDE，

∴，

∴DC2=DEAD，

∵∠DIC=∠DAC+∠ACI，∠DCI=∠ICB+∠DCB，

∵IC平分∠ACB，

∴∠ACI=∠ICB，

∴∠DIC=∠DCI，

∴DC=DI，

∴DI2=DEAD，

∴线段DI是线段DE与DA的比例中项；

所以此选项说法正确；

⑤∵∠BAD=∠DAC，∠BAD=∠DCB，∠DAC=∠DBC，

∴∠DCB=∠DBC，

∴DB=DC，

由④得：DC=DI，

∴DB=DC=DI，

∴点D是△BIC的外心；

所以此选项说法正确；

所以说法正确的有：①③④⑤；

故选D．