题目内容
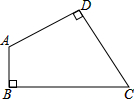 如图,在四边形ABCD中,∠C=60°,∠B=∠D=90°,AD=2AB,CD=3,求BC的长.
如图,在四边形ABCD中,∠C=60°,∠B=∠D=90°,AD=2AB,CD=3,求BC的长.考点:解直角三角形
专题:
分析:延长DA、CB交于点E,解直角三角形求出DE、EC,求出∠E=30°,解直角三角形求出EB,即可求出答案.
解答:解:延长DA、CB交于点E,
∵在Rt△CDE中,tanC=
=
,
cosC=
=
,
∴DE=3
,EC=6,
∵AD=2AB
设AB=k,则AD=2k,
∵∠C=60°,∠B=∠D=90°,
∴∠E=30°,
∵在Rt△ABE中,sinE=
=
tanE=
=
,
∴AE=2AB=2k,EB=
AB=
k,
∴DE=4k=3
,
解得:k=
,
∴EB=
,
∴BC=6-
=
.

∵在Rt△CDE中,tanC=
| DE |
| CD |
| ||
| 2 |
cosC=
| CD |
| EC |
| 1 |
| 2 |
∴DE=3
| 3 |
∵AD=2AB
设AB=k,则AD=2k,
∵∠C=60°,∠B=∠D=90°,
∴∠E=30°,
∵在Rt△ABE中,sinE=
| AB |
| AE |
| 1 |
| 2 |
| AB |
| EB |
| ||
| 3 |
∴AE=2AB=2k,EB=
| 3 |
| 3 |
∴DE=4k=3
| 3 |
解得:k=
3
| ||
| 4 |
∴EB=
| 9 |
| 4 |
∴BC=6-
| 9 |
| 4 |
| 15 |
| 4 |
点评:本题考查了解直角三角形的应用,主要考查学生进行计算的能力,是一道比较好的题目,关键是构造直角三角形.

练习册系列答案
相关题目
对于命题“如果∠1+∠2=90°,那么∠1=∠2.”能说明它是假命题的反例是( )
| A、∠1=45°,2=45° |
| B、∠1=70°,=20° |
| C、∠1=30°,2=40° |
| D、∠1=50°,2=50° |
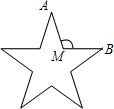 如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出这个五角星,还需要知道∠AMB的度数,那么∠AMB的度数为( )
如图,五角星的五个角都是顶角为36°的等腰三角形,为了画出这个五角星,还需要知道∠AMB的度数,那么∠AMB的度数为( )| A、108° | B、120° |
| C、136° | D、144° |
 如图,反比例函数y=-
如图,反比例函数y=- 已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数
已知:一次函数y=2x+1与y轴交于点C,点A(1,n)是该函数与反比例函数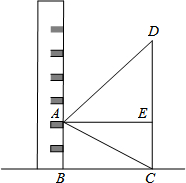 某校数学课题学习小组在“测量旗杆高度”的活动中,站在教学楼上的A处 测得旗杆低端C的俯角为30°,测得旗杆顶端D的仰角为45°,如果旗杆与教学楼的水平距离BC为6m,那么旗杆CD的高度是多少?(结果保留根号)
某校数学课题学习小组在“测量旗杆高度”的活动中,站在教学楼上的A处 测得旗杆低端C的俯角为30°,测得旗杆顶端D的仰角为45°,如果旗杆与教学楼的水平距离BC为6m,那么旗杆CD的高度是多少?(结果保留根号) 如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
如图,AB是⊙O的直径,点C在⊙O上,连接BC,AC,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E. 反比例函数y=
反比例函数y=