题目内容
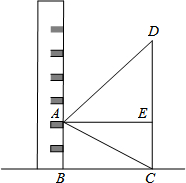 某校数学课题学习小组在“测量旗杆高度”的活动中,站在教学楼上的A处 测得旗杆低端C的俯角为30°,测得旗杆顶端D的仰角为45°,如果旗杆与教学楼的水平距离BC为6m,那么旗杆CD的高度是多少?(结果保留根号)
某校数学课题学习小组在“测量旗杆高度”的活动中,站在教学楼上的A处 测得旗杆低端C的俯角为30°,测得旗杆顶端D的仰角为45°,如果旗杆与教学楼的水平距离BC为6m,那么旗杆CD的高度是多少?(结果保留根号)考点:解直角三角形的应用-仰角俯角问题
专题:
分析:根据在Rt△DAE中,tan∠DAE=
,求出DE的值,再根据在Rt△ACE中,tan∠EAC=
,求出CE的值,最后根据CD=CE+ED,即可求出答案.
| DE |
| AE |
| EC |
| AE |
解答:解:在Rt△DAE中,
∵tan∠DAE=
,
∴tan45°=
,
∴ED=6m,
在Rt△BCD中,
∵在Rt△ACE中,
∵tan∠EAC=
,
∴tan30°=
,
∴CE=2
m,
∴AB=CD=CE+ED=2
+6(m).
答:旗杆的高度是(2
+6)m.
∵tan∠DAE=
| DE |
| AE |
∴tan45°=
| DE |
| 6 |
∴ED=6m,
在Rt△BCD中,
∵在Rt△ACE中,
∵tan∠EAC=
| EC |
| AE |
∴tan30°=
| CE |
| 6 |
∴CE=2
| 3 |
∴AB=CD=CE+ED=2
| 3 |
答:旗杆的高度是(2
| 3 |
点评:此题考查了解直角三角形的应用-仰角俯角问题,本题要求学生借助俯角构造直角三角形,并结合图形利用三角函数解直角三角形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
两个角的大小之比是9:1,它们的差是72°,则这两个角的关系是( )
| A、相等 | B、互补 |
| C、互余 | D、无法确定 |
下面的计算错误的是( )
| A、x4•x4=x16 |
| B、(a3)2=a6 |
| C、b3•b3=b6 |
| D、(-2a)2=4a2 |
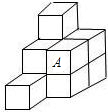 把10个相同的小正方体按如图所示的位置堆放,它的外表含有若干个小正方形.如果将图中标有字母A的一个小正方体搬去.这时外表含有的小正方形个数与搬动前相比( )
把10个相同的小正方体按如图所示的位置堆放,它的外表含有若干个小正方形.如果将图中标有字母A的一个小正方体搬去.这时外表含有的小正方形个数与搬动前相比( )| A、不增不减 | B、减少1个 |
| C、减少2个 | D、减少3个 |
 如图,BP平分∠DBC,CP平分∠ECB,若∠A=α,则∠BPC=
如图,BP平分∠DBC,CP平分∠ECB,若∠A=α,则∠BPC=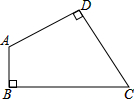 如图,在四边形ABCD中,∠C=60°,∠B=∠D=90°,AD=2AB,CD=3,求BC的长.
如图,在四边形ABCD中,∠C=60°,∠B=∠D=90°,AD=2AB,CD=3,求BC的长.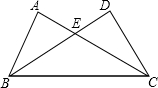 已知:如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
已知:如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.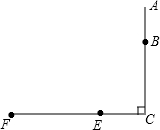 如图,谢明住在一栋住宅楼AC上,他在家里的窗口点B处,看楼下一条公路的两侧点F和点E处(公路的宽为EF),测得俯角α、β分别为30°和60°,点F、E、C在同一直线上.
如图,谢明住在一栋住宅楼AC上,他在家里的窗口点B处,看楼下一条公路的两侧点F和点E处(公路的宽为EF),测得俯角α、β分别为30°和60°,点F、E、C在同一直线上.