题目内容
【题目】已知△ABC的三边长a=3,b=4,c=5,则它的内切圆半径是
【答案】1
【解析】解: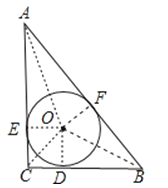
∵a=3,b=4,c=5,
∴a2+b2=c2 ,
∴∠ACB=90°,
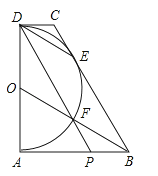
设△ABC的内切圆切AC于E,切AB于F,切BC于D,连接OE、OF、OD、OA、OC、OB,内切圆的半径为R,则OE=OF=OD=R,
∵S△ACB=S△AOC+S△AOB+S△BOC ,
∴![]() ×AC×BC=
×AC×BC=![]() ×AC×0E+
×AC×0E+![]() ×AB×OF+
×AB×OF+![]() ×BC×OD,
×BC×OD,
∴3×4=4R+5R+3R,
解得:R=1.
故答案为:1.
根据勾股定理的逆定理求出△ACB是直角三角形,设△ABC的内切圆切AC于E,切AB于F,切BC于D,连接OE、OF、OD、OA、OC、OB,内切圆的半径为R,则OE=OF=OD=R,根据S△ACB=S△AOC+S△AOB+S△BOC代入即可求出答案.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目