题目内容
【题目】如图所示,已知锐角∠AOB及一点P.
(1)过点P作OA、OB的垂线,垂足分别是M、N;(只作图,保留作图痕迹,不写作法)
(2)猜想∠MPN与∠AOB之间的关系,并证明.

【答案】(1)过点P作OA、OB的垂线PM、PN如图所示见解析;(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB.理由见解析.
【解析】
(1)根据垂线的定义画出图形即可解决问题;
(2)根据四边形内角和为360或“8字型”性质即可解决问题.
解:(1)过点P作OA、OB的垂线PM、PN如图所示;
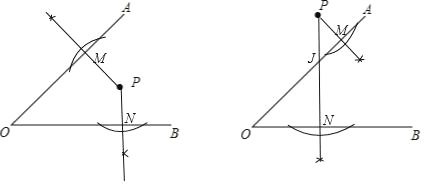
(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB.
理由:左图中,在四边形PMON中,∵∠PMO=∠PNO=90°,
∴∠MPN+∠AOB=180°.
右图中,∵∠PJM=∠OJN,∠AMJ=∠JNO=90°,
∴∠MPN=∠AOB.
故答案为:(1)过点P作OA、OB的垂线PM、PN如图所示见解析;(2)猜想:∠MPN+∠AOB=180°或∠MPN=∠AOB.理由见解析.

练习册系列答案
相关题目