题目内容
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.
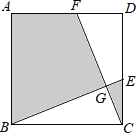
(1)求![]() BGC的度数;
BGC的度数;
(2)若CE=1,H为BF的中点时,求HG的长度;
(3)若图中阴影部分的面积与正方形ABCD的面积之比为2:3,求△BCG的周长.
【答案】(1)90°;(2)![]() ;(3)△BGC的周长为
;(3)△BGC的周长为![]()
【解析】
(1)先利用正方形的性质和SAS证明△BCE≌△CDF,可得∠CBE=∠DCF,再利用角的等量代换即可求出结果;
(2)先根据勾股定理求出BF的长,再利用直角三角形的性质求解即可;
(3)根据题意可得△BCG的面积与四边形DEGF的面积相等,进一步依据△BCG的面积以及勾股定理,得出BG+CG的长,进而求出其周长.
解:(1)∵四边形ABCD是正方形,
∴BC=CD,∠BCD=∠CDF=90°,
在△BCE和△CDF中,∵BC=CD,∠BCD=∠CDF,CE=DF,
∴△BCE≌△CDF(SAS),
∴∠CBE=∠DCF,
又∵∠BCG+∠DCF=90°,
∴∠BCG+∠CBE=90°,
∴∠BGC=90°;
(2)如图,∵CE=1,∴DF=1,∴AF=2,
在直角△ABF中,由勾股定理得:![]() ,
,
∵H为BF的中点,∠BGF=90°,
∴![]() ;
;

(3)∵阴影部分的面积与正方形ABCD的面积之比为2:3,
∴阴影部分的面积为![]() ×9=6,
×9=6,
∴空白部分的面积为9-6=3,
∵△BCE≌△CDF,
∴△BCG的面积与四边形DEGF的面积相等,均为![]() ×3=
×3=![]() ,
,
设BG=a,CG=b,则![]() ab=
ab=![]() ,∴ab=3,
,∴ab=3,
又∵a2+b2=32,
∴a2+2ab+b2=9+6=15,
即(a+b)2=15,
∴a+b=![]() ,即BG+CG=
,即BG+CG=![]() ,
,
∴△BCG的周长=![]() +3.
+3.

【题目】已知二次函数y=ax2﹣bx+c的y与x的部分对立值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣3 | 1 | 3 | 1 |
下列结论①抛物线的开口向下:②其图象的对称轴为x=1:③当x<1时.函数值y随x的增大而增大,④方程ax2+bx+c=0有一个根大于4.其中正确的结论有_____