题目内容
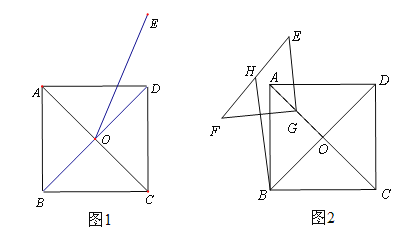
【题目】如图1,正方形ABCD和正方形AEFG,连接DG,BE。
(1)发现
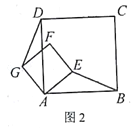
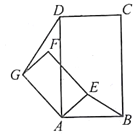
当正方形AEFG绕点A旋转,如图2,①线段DG与BE之间的数量关系是____________。②直线DG与直线BE之间的位置关系是____________。
(2)探究
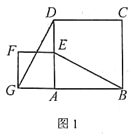
如图3,若四边形ABCD与四边形AEFG都为矩形,且AD=2AB,AG=2AE,证明:直线DG⊥BE
(3)应用
在(2)情况下,连结GE(点E在AB上方),若GE∥AB,且AB=![]() ,AE=1,则线段DG是多少?(直接写出结论)
,AE=1,则线段DG是多少?(直接写出结论)
【答案】 DG=BE DG⊥BE
【解析】试题分析:(1)证明△EAB≌△GAD,可得到BE=DG,∠ABE=∠ADG,再由三角形内角和为180°,即可得到结论;
(2)证明△ABE∽△ADG,再由三角形内角和为180°,即可得到结论;
(3)当GE∥AB时,B、E、F三点在一条直线上,且F刚好在DG上.先求出AD,AG的长,再由勾股定理即可得到结论.
试题解析:解:(1)①DG=BE;②DG⊥BE.理由如下:
延长BE交AD,DG分别为P,H.∵四边形ABCD和四边形AEFG都是正方形,∴AB=AD,∠BAD=90°,AE=AG,∠EAG=90°,∴∠EAB=∠GAD.在△EAB和△GAD中,∵AB=AD,∠EAB=∠GAD,AE=AG,∴△EAB≌△GAD,∴BE=DG,∠ABE=∠ADG.∵∠APB=∠HPD(对顶角相等),∴∠BAP=∠DHP=90°,∴BG⊥DG.
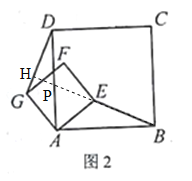
(2)延长BE交AD,DG分别为P,H.
∵∠BAE+∠DAE=∠DAG+∠DAE=90°,∴∠BAE=∠DAG.
∵AD=2AB,AG=2AE,∴![]() ,∴△ABE∽△ADG,∴∠ABP=∠HDP.
,∴△ABE∽△ADG,∴∠ABP=∠HDP.
∵∠APB=∠HPD,∴∠BAD=∠DHP=90°,∴ DG⊥BE.
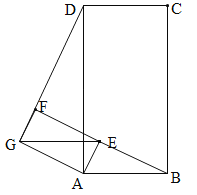
(3) 当GE∥AB时,B、E、F三点在一条直线上,且F刚好在DG上,∴∠AEB=90°.∵∠AGD=∠AEB,∴∠AGD=90°.∵AB=![]() ,AE=1,∴AG=2AE=2,AD=2AB=
,AE=1,∴AG=2AE=2,AD=2AB=![]() ,∴DG=
,∴DG=![]() =
=![]() =4.
=4.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案【题目】全民健身运动已成为一种时尚 ,为了解揭阳市居民健身运动的情况,某健身馆的工作人员开展了一项问卷调查,问卷内容包括五个项目:
A:健身房运动;B:跳广场舞;C:参加暴走团;D:散步;E:不运动.
以下是根据调查结果绘制的统计图表的一部分,
运动形式 | A | B | C | D | E |
人数 |
|
|
|
|
|
请你根据以上信息,回答下列问题:
![]() 接受问卷调查的共有 人,图表中的
接受问卷调查的共有 人,图表中的![]() ,
,![]() .
.
![]() 统计图中,
统计图中,![]() 类所对应的扇形的圆心角的度数是 度.
类所对应的扇形的圆心角的度数是 度.

![]() 揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有
揭阳市环岛路是市民喜爱的运动场所之一,每天都有“暴走团”活动,若某社区约有![]() 人,请你估计一下该社区参加环岛路“暴走团”的人数.
人,请你估计一下该社区参加环岛路“暴走团”的人数.