题目内容
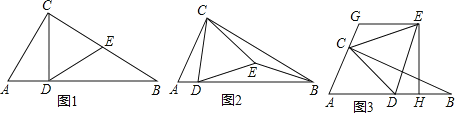
【题目】如图1,等边△ABC中,点D、E分别在BC、AC上,BD=CE,连AD、BE.
(1)求证:△CAD≌△ABE;
(2)如图2,延长FE至点G,使得FG=FA,连AG,试判断△AFG的形状,并说明理由;
(3)在(2)的条件下,连CF,若CF⊥AD,求证:CF⊥CG.

【答案】(1)见解析;(2)见解析.
【解析】
(1)由等边三角形的性质可得:∠BAC=∠ACD=60°,AB=AC=BC,再结合已知得出CD=AE,最后运用SAS即可证明;
(2)由(1)△CAD≌△ABE,可得∠CAD=∠ABE,进而得出∠AFE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,即可说明其为等边三角形;
(3)由(2)知△AFG是等边三角形,进一步说明∠BAF=∠CAG,运用(SAS)判定△ABF≌△ACG,得出∠CGF=∠AGC-∠AGF=60°=∠AFG,则AD∥CG,即可得出结论
解:(1)∵△ABC是等边三角形,
∴∠BAC=∠ACD=60°,AB=AC=BC,
∵BD=CE,
∴CD=AE,
在△CAD和△ABE中,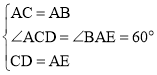 ,
,
∴△CAD≌△ABE(SAS);
(2)由(1)知,△CAD≌△ABE,
∴∠CAD=∠ABE,
∴∠AFE=∠ABE+∠BAD=∠CAD+∠BAD=∠BAC=60°,
∵FG=FA,
∴△AFG是等边三角形;
(3)由(2)知,△AFG是等边三角形,
∴AF=AG,∠AFE=∠AGF=∠FAG=60°=∠BAC,
∴∠BAF=∠CAG,
在△ABF和△ACG中,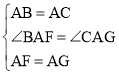 ,
,
∴△ABF≌△ACG(SAS),
∴∠AGC=∠AFB=180°-∠AFG=60°,
∴∠CGF=∠AGC-∠AGF=60°=∠AFG,
∴CG∥AD,
∵CF⊥AD,
∴CF⊥CG.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】市实验中学学生会准备调查七年级学生参加“球类”“书画类”“棋牌类:”“器乐类”四类校本课程的人数.
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时,我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”.这三位同学的调查方式中,最合理的是______(填“甲”“乙”或“丙”)同学的调查方式.
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图,请你根据图表提供的信息解答下列问题:
①a=________,b=________;
②在扇形统计图中,器乐类所对应的圆心角的度数是________;
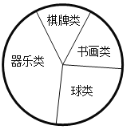
③若该校七年级有学生660人,请你估计大约有多少学生参加球类校本课程?
类别 | 频数(人数) | 百分比 |
球类 | 25 | |
书画类 | 20 | 20% |
棋牌类 | 15 | b |
器乐类 | ||
合计 | a | 100% |