��Ŀ����
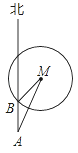
����Ŀ����1����ͼ,��ֱ֪��a��b,��A��ֱ��a��,��B. C��ֱ��b��,��P���߶�AB��,��1=70,��2=100�����PCB�Ķ���.

��2���±���ij����һ����Ʒ���������������Ʒԭ��Ϊ560Ԫ�����Ų�ͬ���ȵĽ��ۣ���λ��Ԫ��������������λ������������Ӧ�仯���±���
���� | 5 | 10 | 15 | 20 | 25 | 30 | 35 |
������ | 78 | 81 | 84 | 87 | 90 | 93 | 96 |
�ٸ��ݱ������г��ı仯��ϵ��������ƽ���֮ǰ���������Ƕ��ټ���
�ڸ��ݱ������г��ı仯��ϵ����ֱ��д��![]() ��
��![]() �Ĺ�ϵʽ.
�Ĺ�ϵʽ.
���𰸡���1��![]() ������2����75������y=
������2����75������y=![]() x+75��
x+75��
��������
��1���ȸ���ƽ���ߵ����ʣ��ó���ABC�Ķ������ٸ���������������ʣ����ɵõ���PCB�Ķ�����
��2���ٸ��ݱ����е����ݣ��ɵý���5Ԫ������3�������ݽ�������������Ĺ�ϵ���ɵô𰸣��ڸ��ݴ���ϵ�������ɵô𰸣�
��1����a��b,��1=70����
���ABC=��1=70����
�ߡ�2=100����
���PCB=��2��ABC=100��70��=30����
�ʴ�Ϊ��![]() ��
��
��2���ɱ��е����ݣ���
��ÿ����5Ԫ������������8178=3����
���ƽ���֮ǰ���������Ƕ��٣�783=75����
��ÿ����5Ԫ������������3��������֮ǰ����������75����
���轵��x(Ԫ)��������y(��)֮��Ĺ�ϵʽΪy=kx+b��
��(5,78)(10,81)���뺯����ϵʽ����
![]()
��� ��
��
����x(Ԫ)��������y(��)֮��Ĺ�ϵʽy=![]() x+75.
x+75.

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�����Ŀ��ijУΪ�˽��ߡ����꼶ѧ����������ˮ����ȫ֪ʶ��������������ߡ����꼶�������ȡ50��ѧ�����в��ԣ����Գɼ����ٷ��ƣ����������������ͷ�����������Ϣ���£�
a�����꼶�ɼ�Ƶ���ֲ�ֱ��ͼ��

b�����꼶�ɼ���![]() ��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
��һ����ǣ�70 72 74 75 76 76 77 77 77 78 79
c���ߡ����꼶�ɼ���ƽ��������λ�����£�
�꼶 | ƽ���� | ��λ�� |
�� | 76.9 | m |
�� | 79.2 | 79.5 |
����������Ϣ���ش��������⣺
��1������β����У����꼶��80�����ϣ���80�֣������� ���ˣ�
��2������m��ֵΪ�� ����
��3������β����У����꼶ѧ��������꼶ѧ���ҵijɼ�����78�֣����ж���λѧ���ڸ����꼶������˭����ǰ����˵�����ɣ�
��4����У���꼶ѧ����400�ˣ�����ȫ���μӴ˴β��ԣ���������꼶�ɼ�����ƽ����76.9�ֵ�������