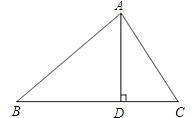
[题目]如图①.如图②均是的正方形网格.每个小正方形顶点叫做格点．的顶点都在格点上．(1)在如图①的网格中找到一个格点.并画出.使与全等.且以点为顶点的四边形只是轴对称图形．(2)在如图②的网格中找到一个格点.并画出.使与全等.且以点为顶点的四边形只是中心对称图形．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图①，如图②均是的正方形网格，每个小正方形顶点叫做格点．的顶点都在格点上．

（1）在如图①的网格中找到一个格点，并画出，使与全等，且以点为顶点的四边形只是轴对称图形．

（2）在如图②的网格中找到一个格点，并画出，使与全等，且以点为顶点的四边形只是中心对称图形．

【答案】（1）答案不唯一，如图①、②见解析；（2）如图③见解析．

【解析】

（1）与全等，有公共边BC，所以有AC=BD，AC=CD两种情况，BC上方可以画1个，BC下方可以画2个，共3个，再根据轴对称图形的概念可以画出图①、②；

（2）根据（1）中的分析，使与全等的可以画3个三角形，再考虑中心对称图形的概念可以画出图③．

（1）答案不唯一，如图①、②

（2）如图③

练习册系列答案

相关题目

【题目】随着科技的发展，某快递公司为了提高分拣包裹的速度，使用机器人代替人工进行包裹分拣，若甲机器人工作，乙机器人工作，一共可以分拣700件包裹；若甲机器人工作，乙机器人工作，一共可以分拣650件包裹.

（1）求甲、乙两机器人每小时各分拣多少件包裹；

（2）去年“双十一”期间，快递公司的业务量猛增，为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件，则它们每天至少要一起工作多少小时？

【题目】（1）如图,已知直线a∥b,点A在直线a上,点B. C在直线b上,点P在线段AB上,∠1=70,∠2=100，求∠PCB的度数.

（2）下表是某商行一种商品的销售情况，该商品原价为560元，随着不同幅度的降价（单位：元），日销量（单位：件）发生相应变化如下表：

降价（元）	5	10	15	20	25	30	35
日销量（件）	78	81	84	87	90	93	96

①根据表格所列出的变化关系，请你估计降价之前的日销量是多少件？

②根据表格所列出的变化关系，请直接写出与的关系式.

【题目】（1）解不等式：，并把它的解集表示在数轴上；

（2）解不等式组，并写出它的所有非负整数解.

【题目】如图，在△ABC中，AD是BC上的高，tanB=cos∠DAC．

（1）求证：AC=BD；

（2）若sin∠C=，BC=12，求AD的长．

【题目】如图，在中，，过点作射线AD//BC，点从点出发沿射线以的速度运动．同时点从点出发沿射线以的速度运动．连结交于点，设点运动时间为．

（1）求证：AG=BG．

（2）求AE+CF的长（用含t的代数式表示）．

（3）设的面积为，直接写出当时，的面积（且含的代数式表示）．

【题目】如图，已知，，点是射线上一动点（与点不重合），、分别平分和，分别交射线于点、.

（1）求的度数；

（2）当点运动时，与之间的数量关系是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由；若变化，请写出变化规律.

（3）当点运动到使时，求的度数.

【题目】已知：如图，正比例函数y＝ax的图象与反比例函数y＝的图象交于点A（3，2）

（1）试确定上述正比例函数和反比例函数的表达式；

（2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？

（3）点M（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点M作直线MB∥x轴，交y轴于点B；过点A作直线AC∥y轴交x轴于点C，交直线MB于点D．当四边形OADM的面积为6时，请判断线段BM与DM的大小关系，并说明理由．

【题目】一家蔬菜公司收购到某种绿色蔬菜200吨，准备加工后进行销售，销售后获利的情况如下表所示：

销售方式	粗加工后销售	精加工后销售
每吨获利（元）	500	800

已知该公司的加工能力是：每天能精加工5吨或粗加工15吨，但两种加工不能同时进行．受季节等条件的限制，公司必须在一定时间内将这批蔬菜全部加工后销售完．

（1）如果要求20天刚好加工完200吨蔬菜，则公司应安排几天精加工，几天粗加工？

（2）如果先进行精加工，然后进行粗加工．

①试求出销售利润W元与精加工的蔬菜吨数m之间的函数关系式；

②若要求在不超过16天的时间内，将200吨蔬菜全部加工完后进行销售，则加工这批蔬菜最多获得多少利润？此时如何分配加工时间？

试题分类