题目内容
【题目】若关于x的方程![]() (a≠0)有两个不相等的实数根,且这两根的值都在1,3之间(含l,3),则a的取值范围是_______。
(a≠0)有两个不相等的实数根,且这两根的值都在1,3之间(含l,3),则a的取值范围是_______。
【答案】![]()
【解析】
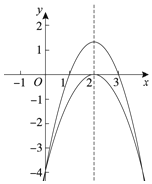
把抛物线解析式配成顶点式可得到抛物线对称轴,从而得到顶点坐标;利用抛物线与x轴的交点问题,可看作抛物线y=ax2-4ax-4(a≠0)与x轴有两个交点,交点的横坐标都在1,3之间(包括1,3),利用二次函数的性质得到抛物线开口向下,顶点在第一象限,所以-4a-4>0且当x=1时,y≤0,即a-4a-4≤0,然后解a的不等式组即可得到a的范围.
解: ∵y=ax2-4ax-4=a(x-2)2-4a-4,
∴抛物线的顶点(2,-4a-4),
∵方程ax2-4ax-4=0(a≠0)有两个不相等的实数根,且两根都在1,3之间(包括1,3),
∴抛物线y=ax2-4ax-4(a≠0)与x轴有两个交点,交点的横坐标都在1,3之间(包括1,3),
∴抛物线开口向下,顶点在第一象限,
∴-4a-4>0,解得a<-1,
当x=1时,y≤0,即a-4a-4≤0,解得a≥-![]() ,
,
∴a的取值范围为![]() .
.
故答案为:![]() .
.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目