题目内容
【题目】如图,矩形OABC摆放在平面直角坐标系![]() 中,点A在
中,点A在![]() 轴上,点C在
轴上,点C在![]() 轴上,OA=8,OC=6.
轴上,OA=8,OC=6.
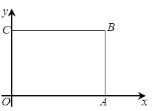

(1)求直线AC的表达式
(2)若直线![]() 与矩形OABC有公共点,求
与矩形OABC有公共点,求![]() 的取值范围;
的取值范围;
(3)若点O与点B位于直线![]() 两侧,直接写出
两侧,直接写出![]() 的取值范围。
的取值范围。
【答案】(1)![]() ;(2)-8<b<6;(3)
;(2)-8<b<6;(3)![]() .
.
【解析】
(1)由条件可先求得A、C两点的坐标,再利用待定系数法可求得直线AC的解析式;
(2)当直线y=x+b过C点和A点时,可求得b的最大值和最小值,可求得b的取值范围;
(3)把点A(0,0),点B(8,6)代入![]() ,求解即可.
,求解即可.
解:(1)∵OA=8,OC=6,
∴A(8,0),C(0,6),
设直线AC解析式为y=kx+m,
把A、C两点坐标代入可得![]() ,
,
解得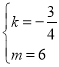 ,
,
∴直线AC的解析式为y=-![]() x+6;
x+6;
(2)由图象可知当直线y=x+b过点C时,把C点坐标代入可得6=0+b,
∴b=6;
当直线y=x+b过点A时,把A点坐标代入可得0=8+b,解得b=-8,
∵若直线y=x+b与矩形OABC有公共点
∴b的取值范围为:-8<b<6,
故答案为: -8<b<6;
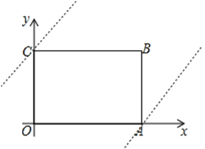
(3)∵OA=8,OC=6,∴B(8,6),
把点A(0,0)代入![]() ,得-2-10k=0,解得:k=-
,得-2-10k=0,解得:k=-![]() ,
,
把点B(8,6)代入![]() ,得8k-2-10k=6 ,解得:k= -4,
,得8k-2-10k=6 ,解得:k= -4,
∴![]() 的取值范围为:
的取值范围为:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目