��Ŀ����
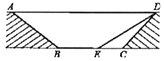
����Ŀ��Ϊ���⽻ͨӵ�£�������ij����ƻ���һ����ͨ������ͨ��һ���ֵĽ�����ͼ��ʾ��ͼ�е���AD��ͨ��BCƽ�У���ͨ��ˮƽ����BCΪ8�ף���BCD=135�㣬ͨ��б��CD �ij�Ϊ6�ף�ͨ��б��AB���¶�i=1��![]()
��1����ͨ��б��AB�ij�Ϊ�����ף�
��2��Ϊ�����������ߵ����ʶȣ��⽫���ͼ�е�ͨ��б��CD���¶ȱ仺���ĺ��ͨ��б��DE���½�Ϊ30�㣬���ʱBE�ij���������������ţ�
���𰸡�(1) 3![]() �ף�(2) ��8+3
�ף�(2) ��8+3![]() ��3
��3![]() ����.
����.
��������
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��������֪�ó�DM=CM=![]() CD=3
CD=3![]() ����AN=DM=3
����AN=DM=3![]() ���ٽ�Rt��ANB����ͨ��б��AB���¶�i=1��
���ٽ�Rt��ANB����ͨ��б��AB���¶�i=1��![]() ���ó�BN=
���ó�BN=![]() AN=6��Ȼ����ݹ��ɶ������AB��
AN=6��Ȼ����ݹ��ɶ������AB��
��2���Ƚ�Rt��MED�����EM=![]() DM=3
DM=3![]() ���ó�EC=EM-CM=3
���ó�EC=EM-CM=3![]() -3
-3![]() ���ٸ���BE=BC-EC������⣮
���ٸ���BE=BC-EC������⣮
��1������A��AN��CB�ڵ�N������D��DM��BC�ڵ�M��
�ߡ�BCD=135�㣬
���DCM=45�㣬
����Rt��CMD�У���CMD=90�㣬CD=6��
��DM= CM= ![]() CD=3
CD=3![]() ��
��
��AN=DM=3 ![]() ��
��
��ͨ��б��AB���¶�i=1��![]() ��
��
��tan��ABN=![]() ��
��
��BN=![]() AN=6��
AN=6��
��AB=![]() =3
=3![]() ��
��
��ͨ��б��AB�ij�ԼΪ3![]() �ף�
�ף�
��2������Rt��MED�У���EMD=90�㣬��DEM=30�㣬DM=3![]() ��
��
��EM=![]() DM=3
DM=3![]() ��
��
��EC=EM��CM=3![]() ��3
��3![]() ��
��
��BE=BC��EC=8����3![]() ��3
��3![]() ��=8+3
��=8+3![]() ��3
��3![]() ��
��
����ʱBE�ij�ԼΪ��8+3![]() ��3
��3![]() ����.
����.







