题目内容
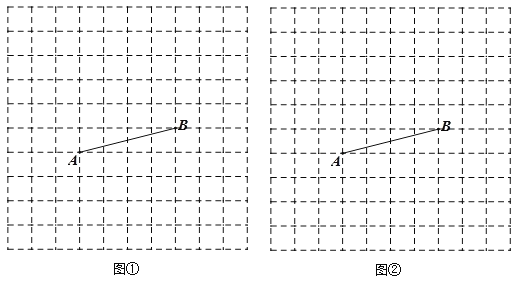
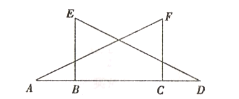
【题目】如图,△ACF≌△DBE,其中点A、B、C、D在一条直线上.
(1)若BE⊥AD,∠F=62°,求∠A的大小.
(2)若AD=9cm,BC=5cm,求AB的长.
【答案】(1)∠A=28°;(2)AB =2 cm.
【解析】
(1)根据全等三角形的性质得到∠FCA=∠EBD=90°,根据直角三角形的性质计算即可;
(2)根据全等三角形的性质得到CA=BD,结合图形得到AB=CD,计算即可.
(1)∵BE⊥AD,
∴∠EBD=90°.
∵△ACF≌△DBE,
∴∠FCA=∠EBD=90°.
∴∠F+∠A=90°
∵∠F =62°,
∴∠A=28°.
(2)∵△ACF≌△DBE,
∴CA=BD.
∴CA-CB=BD-CB.
即AB=CD.
∵AD=9 cm, BC=5 cm,
∴AB+CD=9-5=4 cm.
∴AB=CD=2 cm.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目