题目内容
【题目】已知:抛物线![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 为常数,且
为常数,且![]() )与
)与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)将![]() 平移后得到抛物线
平移后得到抛物线![]() ,点
,点![]() 、
、![]() 在
在![]() 上(点
上(点![]() 在点
在点![]() 的上方),若以点
的上方),若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求抛物线
为顶点的四边形是正方形,求抛物线![]() 的解析式.
的解析式.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]()
【解析】
(1)设交点式![]() ,将
,将![]() 代入,即可求出表达式;
代入,即可求出表达式;
(2)平移抛物线,则a的值不变,设平移后的抛物线![]() 解析式为:
解析式为:![]() ,作出图形,分三种情况讨论,以BC为边作正方形有两种,以BC为对角线作正方形有一种,根据正方形的特点找到D,E坐标,代入
,作出图形,分三种情况讨论,以BC为边作正方形有两种,以BC为对角线作正方形有一种,根据正方形的特点找到D,E坐标,代入![]() 解析式求出a即可.
解析式求出a即可.
(1)∵抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,
∴设交点式![]() ,
,
将![]() 代入得
代入得![]() ,解得
,解得![]()
∴抛物线![]() 的表达式为:
的表达式为:![]()
(2)设平移后的抛物线![]() 解析式为:
解析式为:![]() ,
,
分三种情况讨论:
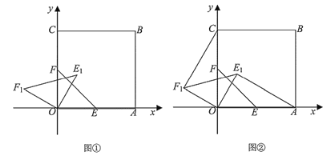
①如图所示,以BC为边作正方形BCED,过E作EH⊥y轴于点H,过D作DG⊥x轴于点G

∵OB=OC=2
∴△OBC为等腰直角三角形
∴∠OBC=∠OCB=45°
又∵∠BCE=90°,∠EHC=90°
∴∠HCE=∠HEC=45°
在△HCE和△OBC中,
∵∠HCE=∠OBC=45°,CE=BC,∠HEC=∠OCB=45°,
∴△HCE≌△OBC(ASA)
∴CH=OB=2,HE=OC=2
∴OH=4
则E点坐标为(2,4)
同理可得D点坐标为(4,2)
将D,E坐标代入![]() 得:
得:
 ,解得
,解得![]()
此时![]() 解析式为:
解析式为:![]() ;
;
②如图所示,以BC为边作正方形BCED
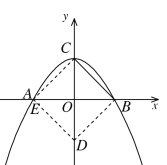
此时E与B关于原点对称,D与C关于原点对称
∴E点坐标为(-2,0),D点坐标为(0,-2)
将D、E坐标代入![]() 得:
得:
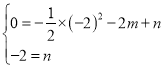 ,解得
,解得![]()
此时![]() 解析式为:
解析式为:![]() ;
;
③以BC为对角线作正方形BDCE
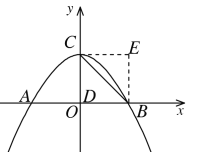
此时D点与原点重合,E点坐标为(2,2)
将D、E坐标代入![]() 得:
得:
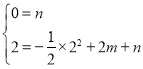 ,解得
,解得![]()
此时![]() 解析式为:
解析式为:![]() ;
;
综上所述,![]() 解析式为:
解析式为:![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目