题目内容
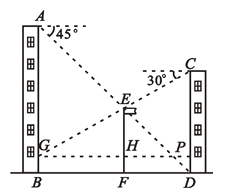
【题目】如图,在楼AB与楼CD之间有一旗杆EF,从AB顶部A点处经过旗杆顶部E点恰好看到楼CD的底部D点,且俯角为45°,从楼CD顶部C点处经过旗杆顶部E点恰好看到楼AB的G点,BG=1米,且俯角为30°,己知楼AB高20米,求旗杆EF的高度.(结果精确到1米)

【答案】8米
【解析】根据题意求出∠BAD=∠ADB=45°,进而根据等腰直角三角形的性质求得FD,在Rt△GEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△AGP中,继而可求出AB的长度.
过点G作![]() 于点P,与EF相交于点H.设EF的长为
于点P,与EF相交于点H.设EF的长为![]() 米,
米,
由题意可知, ![]() 米,
米, ![]() 米,
米,
又∵∠BAD=∠ADB=45°,
∴FD=EF= ![]() 米,AB=BD=20米,
米,AB=BD=20米,
在Rt△GEH中,∠EGH=30°
∵tan∠EGH=![]() ,
,
即![]() ,
,
∴![]() 米,
米,
∵BD=BF+FD=GH+FD,
∴![]()
解得, ![]() ≈8米,
≈8米,
答:旗杆EF的高度约为8米.
“点睛”本题考查了解直角三角形的应用,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目