题目内容
如图,抛物线 经过A
经过A 、C(0,4)两点,与x轴的另一交点是B.
、C(0,4)两点,与x轴的另一交点是B.
(1)求抛物线的解析式;
(2)若点 在第一象限的抛物线上,求点D关于直线BC的对称点
在第一象限的抛物线上,求点D关于直线BC的对称点 的坐标;
的坐标;
(3)在(2)的条件下,过点D作DE⊥BC于点E,反比例函数 的图象经过点E,点
的图象经过点E,点 在此反比例函数图象上,求
在此反比例函数图象上,求 的值.
的值.
(1) ;(2)(0,1);(3)
;(2)(0,1);(3) .
.
解析试题分析:(1)直接利用待定系数法求出抛物线解析式即可.
(2)首先求出D点坐标,进而求出∠DCB=45°=∠BCD,则点D′在y轴上,且CD=CD′=3,即可得出D′点坐标.
(3)首先利用D,D′点坐标得出E点坐标,即可得出反比例函数解析式,进而得出 的值.
的值.
试题解析:(1)∵抛物线 经过A(-1,0)、C(0,4)两点,
经过A(-1,0)、C(0,4)两点,
∴ ,解得:
,解得: .
.
∴抛物线的解析式为: .
.
(2)令 ,解得
,解得 ,
,
∴点B(0,4),OB=4.
∵点 在第一象限的抛物线上,
在第一象限的抛物线上,
∴ ,解得:a1=3,a2=-1.
,解得:a1=3,a2=-1.
∵点 在第一象限,∴a2=-1不合题意舍去.∴a=3.
在第一象限,∴a2=-1不合题意舍去.∴a=3.
∴点D(3,4).
∵C(0,4),∴CD∥x轴,CD=3.
∵OC=4,OB=4,∴∠DCB=45°=∠BCD.
∴点D′在y轴上,且CD=CD′=3.
∴点D′(0,1).
(3)∵点D(3,4),点D′(0,1),∴点E .
.
∴反比例函数解析式为: .
.
∵点F 在反比例函数
在反比例函数 图象上,∴m≠0.
图象上,∴m≠0.
∴ ,即
,即 .
.
∴ .
.
考点:1.二次函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.轴对称的性质;5.求代数式的值.

练习册系列答案
相关题目
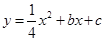 与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC.
与x轴交于点A、B(点A在点B右侧),与y轴交于点C(0,-3),且OA=2OC. 的值;
的值; x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ;
x2对应的碟宽为 ;抛物线y=4x2对应的碟宽为 ;抛物线y=ax2(a>0)对应的碟宽为 ;抛物线y=a(x﹣2)2+3(a>0)对应的碟宽为 ; (a>0)对应的碟宽为6,且在x轴上,求a的值;
(a>0)对应的碟宽为6,且在x轴上,求a的值;

 经过点A(3,2),B(0,1)和点C
经过点A(3,2),B(0,1)和点C .
. ,求点F的坐标;
,求点F的坐标;



 (m是常数)
(m是常数)