题目内容
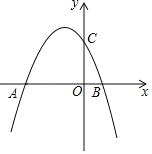
【题目】如图,已知抛物线y=-![]() x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
x2+bx+6与x轴交于点A(﹣6,0)和点B,与y轴交于点C.
(1)求该抛物线的解析式;
(2)写出顶点的坐标,并求AB的长;
(3)若点A,O,C均在⊙D上,请写出点D的坐标,连接BC,并判断直线BC与⊙D的位置关系.
【答案】(1)抛物线的解析式为y=﹣![]() x2﹣x+6;
x2﹣x+6;
(2)AB的长为9;
(3)D点的坐标为(﹣3,3),直线BC与⊙D相交.
【解析】试题分析:(1)根据待定系数法,可得答案;
(2)根据配方法,可得顶点坐标;根据自变量与函数值的对应关系,可得B点坐标,根据两点间的距离,可得答案;
(3)根据直角三角形的斜边大于直角边,可得r与d的关系,根据d<r,可得答案.
试题解析:
(1)将A点坐标代入函数解析式,得
﹣![]() ×(﹣6)﹣6b+6=0,
×(﹣6)﹣6b+6=0,
解得b=﹣1,
该抛物线的解析式为y=﹣![]() x2﹣x+6;
x2﹣x+6;
(2)y=﹣![]() x2﹣x+6配方,得
x2﹣x+6配方,得
y=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
顶点坐标为(﹣![]() ,
, ![]() );
);
当y=0时,﹣![]() x2﹣x+6=0,
x2﹣x+6=0,
解得x=﹣6,x=3,
即A(﹣6,0)B(3,0),
AB的长3﹣(﹣6)=9;
AB的长为9;
(3)点D在AO的中垂线上,CO的中垂线上,
D点的横坐标为![]() =﹣3,D的纵坐标为
=﹣3,D的纵坐标为![]() =3,
=3,
D点的坐标为(﹣3,3);
作DE⊥BC于E如图,
DC>DE,
d>r,
直线BC与⊙D相交.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目