题目内容
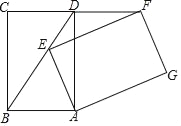
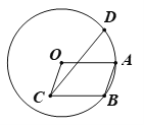
【题目】如图,点A、B在半径为3的⊙O上,以OA、AB为邻边作平行四边形OCBA,作点B关于OA的对称点D,连接CD,则CD的最大值为________.
【答案】3![]() .
.
【解析】
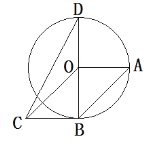
根据点B、D关于OA对称得出BD⊥OA,进而得到BD⊥CB,得出△CBD是直角三角形,CB是固定值,只有当BD最大时CD就最大,转换成求BD的最大值,BD都在圆上,所以BD的最大值就是直径,最后用勾股定理就能求出CD的最大值.
∵平行四边形OCBA,
∴OA∥CB,OA=CB
又∵D是B点关于OA的对称点,
∴DB⊥OA,
∴DB⊥CB,
∴△CBD是直角三角形
∴![]()
∵CB=OA=r=3是固定值
∴DB最大时就是CD最大
而B是圆上的点,D是B对称点且也在圆上
∴当BD经过原点O是直径时最大,即BD=2r=6
∴![]() =
=![]() =45
=45
解得:CD=3![]() ,即CD的最大值是3
,即CD的最大值是3![]() .
.

练习册系列答案
相关题目