题目内容
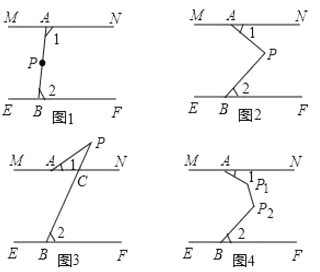
【题目】如图1,将两根笔直的细木条![]() 用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在
用图钉固定并平行摆放,将一根橡皮筋拉直后用图有分别周定在![]() 上,橡皮筋的两端点分别记为点
上,橡皮筋的两端点分别记为点![]() ,点
,点![]() .
.
(1)图1中,点![]() 在
在![]() 上,若
上,若![]() ,则
,则![]() ___________
___________![]() ;
;
(2)![]() 为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使
为橡皮筋上一点,,用橡皮筋的弹性拉动橡皮筋,使![]() 三点不在同一直线,后用图固定点
三点不在同一直线,后用图固定点![]() .
.
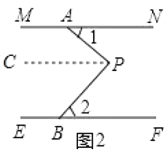
①如图2,若点![]() 在两根细木条所在直线之间,且
在两根细木条所在直线之间,且![]() ,试判断线段
,试判断线段![]() 与
与![]() 所在直线的位置关系,并说明理由;
所在直线的位置关系,并说明理由;
②如图3,若点![]() 在两根细木条所在直线的同侧,且
在两根细木条所在直线的同侧,且![]() ,
,![]() ,试求
,试求![]() 的度数;
的度数;
(3)如图4,![]() 为AB上两点,拉动橡皮筋并固定,若
为AB上两点,拉动橡皮筋并固定,若![]() ,则
,则![]() ____________
____________![]() .
.
【答案】(1) 70;(2)①AP⊥BP,理由见解析;②∠1=31°,∠2=59° (3) 270.
【解析】
(1)根据MN∥EF即可得出∠1+∠2=180°,结合∠1=110°即可求出∠2的度数;
(2)①过点P作PC∥MN,根据MN∥EF即可得出PC∥MN∥EF,进而得出∠APC=∠1,∠BPC=∠2再根据角与角之间的关系即可得出∠APB=∠1+∠2=90°,由此即可得出AP⊥BP;
②2过点P作PD∥MN,同理可得出∠APC=∠1,∠BP=∠2,根据角与角之间的关系即可得出∠APB=∠2-∠1=28°,再结合∠1+∠2=90°,即可求出∠1、∠2的度数;
(3)过点P作P1C∥MN,过点P2作P2D∥MN,由MN∥EF即可得出P1c∥MN∥EF∥P2D,从而可得出∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°,再根据角与角之间的关系即可算出∠AP1P2+∠BP2P1的度数.
(1)∵MN∥EF,
∴∠1+∠2=180°,
∵∠1=110°,
∴∠2=70°
故答案为:70.
(2)①AP⊥BP,理由如下
在图2中,过点P作PC∥MN,
∵MN∥EF,
∴PC∥MN∥EF,
∴∠APC=∠1,∠BPC=∠2.
∵∠APB=∠APC+∠BPC,∠1+∠2=90°,
∴∠APB=90°,
∴AP⊥BP.
②在图3中,过点P作PD∥MN,
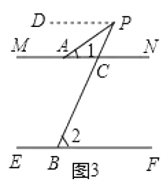
∵MN∥EF,
∴PD∥MN∥EF,
∴∠DPA=∠1,∠DPB=∠2,
∴∠APB=∠DPB-∠DPA=∠2-∠1=28°
又∵∠1+∠2=90°,
∴∠1=31°,∠2=59°
(3)在图4中,过点P作PC∥MN,过点P2作P2D∥MN,
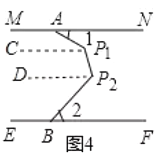
∵MN∥EF,
∴P1C∥MN∥EF∥P2D,
∴∠1=∠AP1C,∠2=∠BP2D,∠CP1P2+∠DP2P1=180°,
又∵∠1+∠2=90°,
∴∠AP1P2+∠BP2P1=∠AP1C+∠CP1P2+∠BP2D+∠BP2P1
=(∠AP1C+∠BP2D)+( ∠CP1P2+∠DP2P1)=90°+180°=270°
故答案为:270.