题目内容
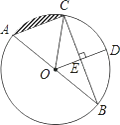
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE.
(1)若CB=4,BE=5,求AE的长;
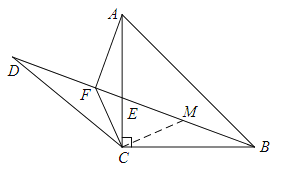
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC;
小洁在遇到此问题时不知道怎么下手,秦老师提示他可以过点C作CH![]() CF,交DB于点H,先证明△AFC
CF,交DB于点H,先证明△AFC![]() △BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.
△BHC,然后继续思考,并鼓励小洁把证明过程写出来.请你帮助小洁完成这个问题的证明过程.

【答案】(1)1;(2)详见解析.
【解析】
(1)根据等腰直角三角形的性质求出AC和BC的长,由勾股定理求出CE的长,再根据AE=AC-CE即可求出AE的长;
(2)过点C作CM⊥CF交BD于点M,先通过证△ACF≌△BCM,得出FC=MC,∠CFM=45°,进而得出∠AFC=∠DFC,结合已知条件可证△ACF≌△DCF,从而可得AC=DC,通过等量代换可得DC=BC.
(1)在△ABC中,
CE=![]() =3
=3
∴AE=AC-CE=4-3=1.
(2)如图,过点C作CM⊥CF交BD于点M.
∴∠FCM=90°,
∵∠ACB=90°,
∴∠FCA=∠MCB,
∵AF⊥BD,
∴∠AFB=90°,
∴∠AFE=∠ACB,
∵∠AEF=∠BEC,
∴∠CAF=∠CBM,
在△ACF和△BCM中,
∵∠FCA=∠MCB,
AC=BC,
∠CAF=∠CBM,
∴△ACF≌△BCM
∴FC=MC,
又∵∠FCM=90°,
∴∠CFM=∠CMF=45°,
∴∠AFC=90°+45°=135°,∠DFC=180°-45°=135°,
∴∠AFC=∠DFC.
在△ACF和△DCF中,
∵AF=DF,
∠AFC=∠DFC,
CF=CF,
∴△ACF≌△DCF,
∴AC=DC,
∵AC=BC,
∴DC=BC.

【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ① |
平均步长(米/步) | 0.6 | ② |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.