题目内容
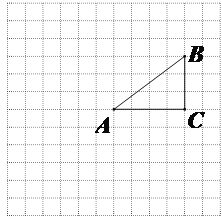
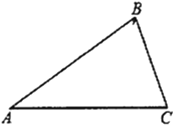
【题目】如图,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线.
的角平分线.
(1)尺规作图:在图中作出角平分线![]() ,交
,交![]() 于点
于点![]() (要求保留作图痕迹,不写作法);
(要求保留作图痕迹,不写作法);
(2)已知![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的周长.
的周长.
【答案】(1)作图见解析;(2)△CDE的周长为13cm.
【解析】
(1)根据角平分线的作法作出BD即可;
(2)根据等腰三角形的性质可得∠ABC=∠C,根据平行线的性质可得∠ABC=∠DEC,即可证明∠DEC=∠C,可得CD=DE,进而可求出△CDE的周长.
(1)如图,以点B为圆心,任意长为半径画弧,交AB、BC于点M、N,分别以M、N为圆心,大于![]() MN长为半径画弧,两弧交于点P,作射线BP,交AC于D,BD即为所求.
MN长为半径画弧,两弧交于点P,作射线BP,交AC于D,BD即为所求.

(2)如(1)中图,DE//AB,
∵AB=AC,
∴∠ABC=∠C,
∵DE//AB,
∴∠ABC=∠DEC,
∴∠DEC=∠C,
∴DE=CD,
∵DE=5cm,CE=3cm,
∴△CDE的周长=CD+DE+CE=5+5+3=13cm.

练习册系列答案
相关题目
【题目】为了对某市区全民阅读状况进行调查和评估,有关部门随机抽取了部分市民进行每天阅读时间情况的调查,并根据调查结果制做了如下尚不完整的频数分布表(被调查者每天的阅读时间均在0﹣120分钟之内)
阅读时间x(分钟) | 0≤x<30 | 30≤x<60 | 60≤x<90 | 90≤x≤120 |
频数 | 450 | 400 | m | 50 |
频率 | 0.45 | 0.4 | 0.1 | n |
(1)被调查的市民人数为多少,表格中,m,n为多少;
(2)补全频数分布直方图;
(3)某市区目前的常住人口约有118万人,请估计该市区每天阅读时间在60~120分钟的市民大约有多少万人?