题目内容
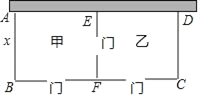
【题目】林场要建一个果园(矩形ABCD),果园的一面靠墙(墙最大可用长度为30米),另三边用木栏围成,中间EF也用木栏隔开,分为甲、乙两个场地,并在如图所示的三处各留1米宽的门(不用木栏),木栏总长57米.设果园(矩形ABCD)的宽AB为x米,矩形ABCD的面积为S平方米.
(1)求S关于x的函数表达式,并写出自变量x的取值范围.
(2)求果园能达到的最大面积S及相应x的值.
(3)若木栏BF比CF多10米,其余条件不变,甲场地种植葡萄,一季平均每平方米收益40元;乙场地种植益莓,一季平均每平方米收益160元.问该果园一季能达到的最大收益W为多少元?
【答案】(1)S=﹣3x2+60x ,10≤x<20(2)300m2(3)24000元
【解析】
(1)由AB=x得出BC=60﹣3x,再根据矩形的面积公式可得函数解析式;
(2)将(1)中所得函数解析式配方成顶点式,利用二次函数的性质解答即可;
(3)由BC=60﹣3x且木栏BF比CF多10米得出BF=![]() +5=35﹣1.5x,CF=
+5=35﹣1.5x,CF=![]() ﹣5=25﹣1.5x,根据“总收益=葡萄总收益+益莓总收益”列出函数解析式,继而利用二次函数的性质求解可得.
﹣5=25﹣1.5x,根据“总收益=葡萄总收益+益莓总收益”列出函数解析式,继而利用二次函数的性质求解可得.
(1)由题意可知,∵AB=x,
∴BC=60﹣3x.
∴S=x(60﹣3x)=﹣3x2+60x.
由BC=60﹣3x≤30,且60﹣3x>0,
可得自变量x的取值范围是:10≤x<20.
(2)因为S=﹣3x2+60x=﹣3(x﹣10)2+300,
所以x=﹣![]() =10m时,S最大值=300m2.
=10m时,S最大值=300m2.
(3)∵BC=60﹣3x,即BF+CF=60﹣3x,
∴BF=![]() +5=35﹣1.5x,CF=
+5=35﹣1.5x,CF=![]() ﹣5=25﹣1.5x.
﹣5=25﹣1.5x.
∴W=40x(35﹣1.5x)+160x(25﹣1.5x)
=﹣300x2+5400x (10≤x<![]() ),
),
x=﹣![]() =9,但不在取值范围内,
=9,但不在取值范围内,
由函数增减性可知,当x=10m时,W最大=24000元.
答:该果园一季能达到的最大收益W为24000元.

 阅读快车系列答案
阅读快车系列答案