题目内容
一位同学拿了两块45°三角尺△MNK,△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=4.

(1)如图(1),两三角尺的重叠部分为△ACM,则重叠部分的面积为 ,
(2)将图(1)中的△MNK绕顶点M逆时针旋转45°,得到图(2),此时重叠部分的面积为 ,
(3)如果将△MNK绕M旋转到不同于图(1)和图(2)的图形,如图(3),请你求此时重叠部分的面积

(1)如图(1),两三角尺的重叠部分为△ACM,则重叠部分的面积为 ,
(2)将图(1)中的△MNK绕顶点M逆时针旋转45°,得到图(2),此时重叠部分的面积为 ,
(3)如果将△MNK绕M旋转到不同于图(1)和图(2)的图形,如图(3),请你求此时重叠部分的面积
(1)4;(2)4;(3)4.
试题分析:(1)利用勾股定理列式求出AB,再根据等腰直角三角形的性质可得CM⊥AB,AM=CM=
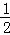 AB,然后求解即可;
AB,然后求解即可;(2)设MN与AC的交点为D,BC与MK的交点为G,根据旋转角是45°求出∠AMD=45°,然后根据同位角相等,两直线平行求出DM∥BC,从而判定DM是△ABC的中位线,然后求出DM=
 BC,同理求出MG=
BC,同理求出MG= AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积即可;
AC,判断出四边形DCGM是正方形,再根据正方形的性质求出面积即可;(3)过点M作ME⊥AC于E,作MF⊥BC于F,可得四边形ECMF是正方形,根据正方形的性质可得ME=MF,再根据同角的余角相等求出∠DME=∠GMF,然后利用“角边角”证明△DME和△GMF全等,根据全等三角形面积相等可得△DME和△GMF的面积相等,然后求出阴影部分的面积等于正方形ECMF的面积,根据三角形的中位线平行于第三边并且等于第三边的一半求出ME,然后求解即可.
试题解析:(1)∵AC=BC=4,∴AB=
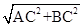 =
=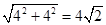 ,∵M是AB的中点,∴CM⊥AB,AM=CM=
,∵M是AB的中点,∴CM⊥AB,AM=CM=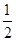 AB=
AB=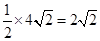 ,∴阴影部分的面积=
,∴阴影部分的面积=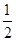 AM•CM=
AM•CM=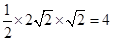 ;
;(2)设MN与AC的交点为D,BC与MK的交点为G,∵旋转角是45°,∴∠AMD=45°,又∵△ABC是等腰直角三角形,∴∠B=45°,∴∠AMD=∠B=45°,∴DM∥BC,∵M是AB的中点,∴DM是△ABC的中位线,∴DM=
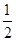 BC=
BC=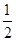 ×4=2,同理可得,MG=
×4=2,同理可得,MG=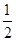 AC=
AC=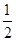 ×4=2,∴四边形DCGM是正方形,∴阴影部分的面积=22=4;
×4=2,∴四边形DCGM是正方形,∴阴影部分的面积=22=4;(3)如图,过点M作ME⊥AC于E,作MF⊥BC于F,∵M是等腰直角△ABC斜边AB的中点,∴四边形ECMF是正方形,∴ME=MF,∵∠DME+∠EMG=∠NMK=90°,∠GMF+∠EMG=∠EMF=90°,∴∠DME=∠GMF,在△DME和△GMF中,
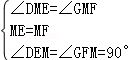 ,∴△DME≌△GMF(ASA),∴S△DME=S△GMF,∴阴影部分的面积=正方形ECMF的面积,∵M是AB的中点,∴ME是△ABC的中位线,∴ME=
,∴△DME≌△GMF(ASA),∴S△DME=S△GMF,∴阴影部分的面积=正方形ECMF的面积,∵M是AB的中点,∴ME是△ABC的中位线,∴ME=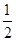 BC=
BC=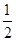 ×4=2,∴正方形ECMF的面积=22=4,∴阴影部分的面积=4.
×4=2,∴正方形ECMF的面积=22=4,∴阴影部分的面积=4.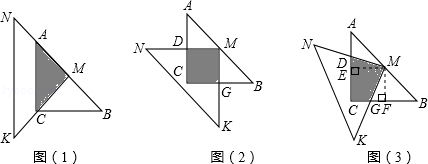

练习册系列答案
相关题目


