��Ŀ����
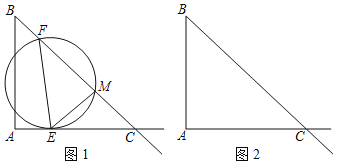
����Ŀ����2013���Ĵ�����11�֣���һ���߳�Ϊa����λ��cm����������ABCD�У���E��M�ֱ����߶�AC��CD�ϵĶ��㣬����DE���ӳ��������εı��ڵ�F������M��MN��DF��H����AD��N��
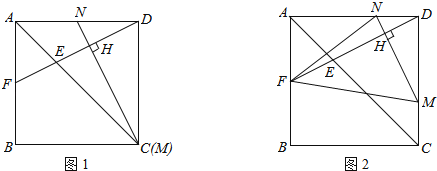
��1����ͼ1������M���C�غϣ���֤��DF=MN��
��2����ͼ2�������M�ӵ�C��������1cm/s���ٶ���CD���D�˶�����Eͬʱ�ӵ�A��������![]() cm/s�ٶ���AC���C�˶����˶�ʱ��Ϊt��t��0����
cm/s�ٶ���AC���C�˶����˶�ʱ��Ϊt��t��0����
���ж����⡰����F�DZ�AB�е�ʱ�����M�DZ�CD�����ȷֵ㡱����٣���˵�����ɣ�
������FM��FN����MNF�ܷ�Ϊ���������Σ����ܣ���д��a��t֮��Ĺ�ϵ�������ܣ���˵�����ɣ�
���𰸡��⣺��1��֤�����ߡ�DNC+��ADF=90�㣬��DNC+��DCN=90�㣬���ADF=��DCN��
����ADF����DNC����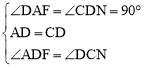 ��
��
���ADF�ա�DNC��ASA������DF=MN��
��2�����������������⡣�������£�
����F�DZ�AB�е�ʱ����AF=![]() AB=
AB=![]() CD��
CD��
��AB��CD�����AFE�ס�CDE��
��![]() ����AE=
����AE=![]() EC����AE=
EC����AE=![]() AC=
AC=![]() a����
a����![]() ��
��
��CM=1t=![]() a=
a=![]() CD��
CD��
����MΪ��CD�����ȷֵ�
�������������£�
��֤AFE�ס�CDE����![]() ����
����![]() ����
����![]() ��
��
��֤��MND�ס�DFA����![]() ����
����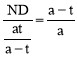 ����ND=t��
����ND=t��
��ND=CM=t��AN=DM=a��t��
����MNF�������������������������
��I����FN=MN������AN=DM֪��FAN�ա�NDM��
��AF=DM����![]() =t����t=0���������������������������
=t����t=0���������������������������
��II����FN=FM����MN��DF֪��HN=HM����DN=DM=MC��
��t=![]() a����ʱ��F���B�غ���
a����ʱ��F���B�غ���
��III����FM=MN����Ȼ��ʱ��F��BC���ϣ���ͼ��ʾ��
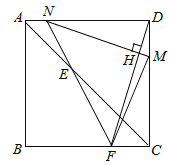
����MFC�ա�NMD����FC=DM=a��t��
������NDM�ס�DCF����![]() ����
����![]()
��![]() ��
��
��![]() =a��t��
=a��t��
��t=a����ʱ��F���C�غ���
������������t=a��t=![]() aʱ����MNF�ܹ���Ϊ������������
aʱ����MNF�ܹ���Ϊ������������
����������1��֤����ADF�ա�DNC�����ɵõ�DF=MN��
��2��������֤����AFE�ס�CDE�����ñ���ʽ���ʱ��t=![]() a�������õ�CM=
a�������õ�CM=![]() a=
a=![]() CD�����Ը�����Ϊ��������
CD�����Ը�����Ϊ��������
������MNFΪ���������Σ���������������Σ���Ҫ����������