题目内容
【题目】利用无刻度的直尺和圆规作出符合要求的图形.(注:不要求写作法,但保留作图痕迹)
(1)如图,已知线段AB,作一个△ABC,使得∠ACB=90°;(只需画一个即可)
(2)如图,已知线段MN,作一个△MPN,使得∠MPN=90°且sinM=![]() .(只需画一个即可)
.(只需画一个即可)

(1) (2)
【答案】(1)作图见解析.(2)作图见解析.
【解析】分析:(1)作线段AB的垂直平分线MN,交AB于点O,以O为圆心OA为半径作⊙O,在⊙O上任意取一点C,连接AC、BC即可;
(2)作等边三角形△PMN,以MN为直径作⊙O,过点N作NF⊥MN,作∠PMN的平分线交NF于H,作∠MHN的平分线HB交MN于B,则BM=HM=2BN,以N为圆心NB为半径作弧交⊙O于P,连接MP、PN,△PMN即为所求.
详解:解:(1)如图△ABC即为所求;
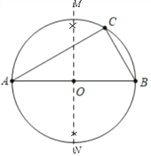
(2)△PMN即为所求;
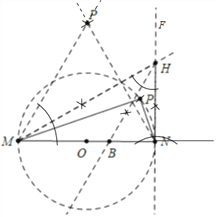

练习册系列答案
相关题目