题目内容
【题目】如图，在□ABCD中，E、F分别是AD、BC的中点，∠AEF的角平分线交AB于点M，∠EFC的角平分线交CD于点N，连接MF、NE．
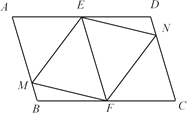
（1）求证：四边形EMFN是平行四边形．
（2）小明在完成（1）的证明后继续进行了探索，他猜想：当AB＝AD时，四边形EMFN是矩形．请在下列框图中补全他的证明思路．
【答案】（1）见解析；（2）∠EFM＝∠BMF，AM＝BM（或：M是AB中点）．
【解析】
（1）根据平行四边形的性质可得∠A=∠C，∠AEF＝∠CFE，AD=BC，根据角平分线的定义和中点的定义可得∠AEM＝∠CFN，AE＝CF，利用ASA即可证明△AME≌△CNF，可得EM＝FN，∠FEM＝∠FEN，根据内错角相等可得EM//FN，即可证明四边形EMFN是平行四边形；（2）由AE=BF，AE//BF可得四边形ABFE是平行四边形，可得EF//AB，可得∠MEF=∠AME，∠EFM=∠BMF，由角平分线可得∠AEM=∠MEF，即可证明∠AEM=∠AME，可得AE=AM，由AB=AD可得M为AB中点，即可证明BM=BF，进而可得∠BMF=∠BFM，即可证明∠BFM=∠EFM，可得∠EFM+∠EFN=90°，可得四边形EMFN是矩形．
(1)在□ABCD中，∠A＝∠C，AD∥BC，AD＝BC
∵E、F分别是AD、BC的中点，
∴AE＝
AD，CF＝BC，
又∵AD＝BC，
∴AE＝CF，
∵AD∥BC，
∴∠AEF＝∠CFE，
∵EM平分∠AEF，FN平分∠EFC，
∴∠AEM＝∠FEM＝∠AEF，∠CFN＝∠FEN＝∠CFE，
∵∠AEF＝∠CFE，∠AEM＝∠AEF，∠CFN＝∠CFE，
∴∠AEM＝∠CFN，
在△AME和△CNF中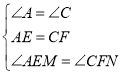
，
∴△AME≌△CNF（ASA），
∵∠FEM＝∠FEN，
∴EM∥FN，
∵△AME≌△CNF，
∴EM＝FN，
∵EM∥FN，EM＝FN，
∴四边形EMFN是平行四边形．
（2）∵AE=BF，AE//BF，
∴四边形ABFE是平行四边形，
∴AB//EF，
∴∠MEF=∠AME，∠EFM=∠BMF，
∵∠AEM=∠MEF，
∴∠AEM=∠AME，
∴AE=AM，
∵E为AD中点，AB=AD，
∴M为AB中点，即AM=BM，
∵AE=BF，
∴BM=BF，
∴∠BMF=∠BFM，
∴∠BFM=∠EFM，
∵∠EFN=∠CFN，
∴∠EFM+∠EFN=90°，即∠MFN=90°，
∴四边形EMFN是矩形．
故答案为：∠EFM＝∠BMF，AM＝BM（或：M是AB中点）．
