题目内容
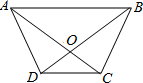 如图 AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是
如图 AB∥CD,AD不平行于BC,AC与BD相交于点O,写出三对面积相等的三角形是△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
△ADC和△BDC;△ADO和△BCO;△DAB和△CAB
.分析:过D作DM⊥AB于M,过C作CN⊥AB于N,得出四边形DMNC是平行四边形,求出DM=CN,设DM=CN=h,根据三角形的面积公式求出即可.
解答:解:△ADC和△BDC,△ADO和△BCO,△DAB和△CAB,理由是: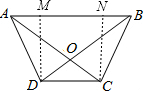
过D作DM⊥AB于M,过C作CN⊥AB于N,
则DM∥CN,
∵AB∥CD,
∴四边形DMNC是平行四边形,
∴DM=CN,
设DM=CN=h,
∴S△ADC=
×DC×h,S△BDC=
×DC×h,
∴S△ADC=S△BDC,
同理S△DAB=S△CAB,
∴S△DAB-S△DOC=S△CAB-S△DOC,
∴S△ADO=S△BCO.
故答案为:△ADC和△BDC,△ADO和△BCO,△DAB和△CAB.

过D作DM⊥AB于M,过C作CN⊥AB于N,
则DM∥CN,
∵AB∥CD,
∴四边形DMNC是平行四边形,
∴DM=CN,
设DM=CN=h,
∴S△ADC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△ADC=S△BDC,
同理S△DAB=S△CAB,
∴S△DAB-S△DOC=S△CAB-S△DOC,
∴S△ADO=S△BCO.
故答案为:△ADC和△BDC,△ADO和△BCO,△DAB和△CAB.
点评:本题考查了平行线间的距离和三角形的面积,平行四边形的性质和判定等知识点,主要应用了等底等高的三角形的面积相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
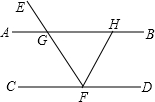 已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,求:∠BHF的度数.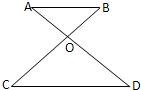 4、如图AB∥CD,AD、BC交于点O,∠A=42°,∠C=58°,则∠AOB=( )
4、如图AB∥CD,AD、BC交于点O,∠A=42°,∠C=58°,则∠AOB=( )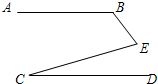 4、如图AB∥CD,∠ABE=120°,∠ECD=25°,则∠E=( )
4、如图AB∥CD,∠ABE=120°,∠ECD=25°,则∠E=( )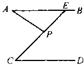
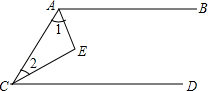 完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.
完成填空,如图AB∥CD,AE平分∠BAC,CE平分∠ACD.求证:AE⊥CE.