题目内容
两个三角形的两条边和其中一边上的高对应相等,则这两个三角形第三边所对的角的关系是( )
| A.不相等 | B.相等 | C.互补或相等 | D.互余 |
C
根据题意,写出已知、并画出图形,分两种情况,首先得出AH=EG,然后证明△ACH≌△EDG,根据全等三角形的性质和邻补角的性质,即可得出.
如图,已知AC=DE,AB=EF,CH=DG,CH⊥AB,DG⊥EF;
求∠A与∠E的关系.
解:①如图,根据题意,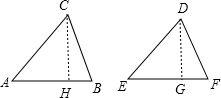
∵AC=DE,CH=DG,CH⊥AB,DG⊥EF,
∴根据勾股定理,可得AH=EG,
在△ACH和△EDG中,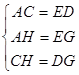 ,
,
∴△ACH≌△EDG,
∴∠A=∠E;
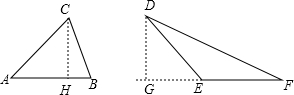
②如图,
∵AC=DE,CH=DG,CH⊥AB,DG⊥EF,
∴AH=EG,
在△ACH和△EDG中,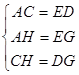 ,
,
∴△ACH≌△EDG,
∴∠A=∠DEG,
∵∠DEG+∠DEF=180°,
∴∠A+∠DEF=180°.
故选C.
本题主要考查了全等三角形的性质和勾股定理,注意要分两种情况解答,不要遗漏.
如图,已知AC=DE,AB=EF,CH=DG,CH⊥AB,DG⊥EF;
求∠A与∠E的关系.
解:①如图,根据题意,

∵AC=DE,CH=DG,CH⊥AB,DG⊥EF,
∴根据勾股定理,可得AH=EG,
在△ACH和△EDG中,
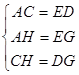 ,
,∴△ACH≌△EDG,
∴∠A=∠E;

②如图,
∵AC=DE,CH=DG,CH⊥AB,DG⊥EF,
∴AH=EG,
在△ACH和△EDG中,
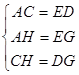 ,
,∴△ACH≌△EDG,
∴∠A=∠DEG,
∵∠DEG+∠DEF=180°,
∴∠A+∠DEF=180°.
故选C.
本题主要考查了全等三角形的性质和勾股定理,注意要分两种情况解答,不要遗漏.

练习册系列答案
相关题目
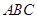 中,
中,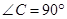 ,EF//AB,
,EF//AB,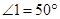 ,则
,则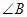 的度数为( )
的度数为( )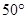
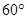
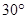
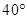
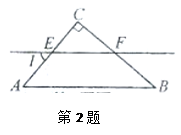
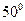 的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成
的角度射向斜放在地面AB上的平面镜CD,经平面镜反射后与水平面成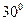 的角,则CD与地面AB 所成的角
的角,则CD与地面AB 所成的角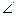 CDA 的度数是
CDA 的度数是