题目内容
若a、b、c是三角形三边的长，则代数式（a-b）2-c2的值是
- A.大于零
- B.小于零
- C.大于或等于零
- D.小于或等于零
B
分析：根据三角形任意两边之和大于第三边可得a+c＞b，a＜b+c，整理可得a+c-b＞0，a-b-c＜0，而（a-b）2-c2=（a-b+c）（a-b-c），那么可知乘积结果小于0．
解答：根据题意可得
a+c＞b，a＜b+c，
即a+c-b＞0，a-b-c＜0，
∵（a-b）2-c2=（a-b+c）（a-b-c），
∴（a-b）2-c2＜0，
故选B．
点评：本题考查了因式分解、三角形三边关系，解题的关键是知道三角形任意两边之和大于第三边．
分析：根据三角形任意两边之和大于第三边可得a+c＞b，a＜b+c，整理可得a+c-b＞0，a-b-c＜0，而（a-b）2-c2=（a-b+c）（a-b-c），那么可知乘积结果小于0．
解答：根据题意可得
a+c＞b，a＜b+c，
即a+c-b＞0，a-b-c＜0，
∵（a-b）2-c2=（a-b+c）（a-b-c），
∴（a-b）2-c2＜0，
故选B．
点评：本题考查了因式分解、三角形三边关系，解题的关键是知道三角形任意两边之和大于第三边．
练习册系列答案
相关题目
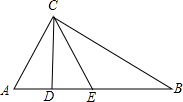如图，△ABC中，∠ACB=90°，CD、CE分别为斜边AB上的高和中线，若∠B=30°，则△ACE是