题目内容
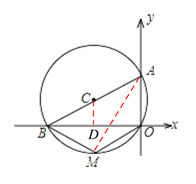
【题目】如图，⊙C过原点O，且与两坐标轴分别交于点A、B，点A的坐标为（0，2），M是第三象限内⊙C上一点，∠BMO=120°，则圆心C的坐标为（ ）
A. （1，1） B. （1， 
） C. （2，1） D. （﹣
，1）
【答案】D
【解析】如图，连接AM，过点C作CD⊥OB于点D，由题意可知，∠AOB=90°，OA=2，
∵在△OBM中，∠BMO=120°，
∴∠MBO+∠MOB=180°-120°=60°，
∵∠MAB=∠MOB，∠MAO=∠MBO，∠BAO=∠MAB+∠MAO，
∴∠BAO=60°，
又∵∠AOB=90°，
∴∠ABO=30°，AB是⊙C的直径，
∴AB=2AO=4，BO=
，BC=2，
∵CD⊥OB于点D，
∴OD=
OB=
，CD=
BC=1，
∴点C的坐标为： 
.
故选D.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
