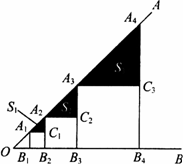
题目内容
| |||||
答案:
解析:
解析:
|
解:(1)BE=DF.理由如下: ∵四边形ABCD是正方形, ∴BC=DC,∠BCE=∠DCF=90°, 又∵CE=CF, ∴△BCE≌△DCF, ∴BE=DF. (2)由(1)知,△BCE≌DCF, ∴∠BEC=∠DFC=60°, ∵∠DCF=90°,CE=CF, ∴∠CFE=45°, ∴∠EFD=∠DFC-∠CFF=15°. |

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
| |||||