Question

（11·孝感）已知正方形ABCD，以CD为边作等边△CDE，则∠AED的度数是__________.

Answer 1

15°或75°

由图1和图2根据正方形的性质和等边三角形的性质就可以求出△ADE是等腰三角形，再由等边三角形的性质就可以求出结论．
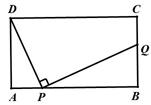
解：如图1，当△CDE在正方形外部时，
∵四边形ABCD是正方形，
∴AD=DC，∠ADC=90°，
∵△CDE是等边三角形，
∴CD=DE，∠CDE=60°
∴AD=DE，∠ADE=150°，
∴∠DAE=∠DEA．
∵∠DEA+∠DAE+∠ADE=180°，
∴∠AED=15°．
如图2，当△CED在正方形内部时，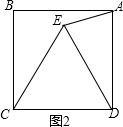
∵四边形ABCD是正方形，
∴AD=DC，∠ADC=90°，
∵△CDE是等边三角形，
∴CD=DE，∠CDE=60°
∴AD=DE，∠ADE=30°，
∴∠DAE=∠DEA．，
∵∠DEA+∠DAE+∠ADE=180°，
∴∠AED=75°．
本题考查了正方形的性质的运用，等腰三角形的性质的运用，等边三角形的性质的运用．解答时求出AD=DE是关键．