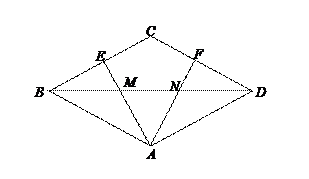题目内容
（11·曲靖）已知△ABC中，DE∥BC，EF∥AB，AB＝3，BC＝6，AD:DB＝2:1，
则四边形DBFE的周长为_______．
则四边形DBFE的周长为_______．
10
分析：根据DE∥BC可以得到△ADE∽△ABC，利用相似三角形对应边成比例求出DE的长度，再根据EF∥AB得到△ABC∽△EFC并且求出CE：AC的值，利用相似三角形对应边成比例求出EF的长度，然后证明四边形DBFE是平行四边形，两邻边之和的2倍就是四边形的周长．
解答：解：∵AD：DB=2：1，
∴
，
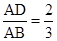∵DE∥BC，
∴△ADE∽△ABC，
∴
，
∴DE=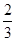
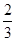×BC=×6=4，
∵DE∥BC，
∴
，
∴
，
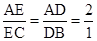又∵EF∥AB，
∴
，
∵AB=3，
∴EF=AB×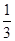
=1，
∵DE∥BC，EF∥AB，
∴四边形DBFE是平行四边形，
∴四边形DBFE的周长=2（DE+EF）=2（4+1）=10．
故答案为：10．
解答：解：∵AD：DB=2：1，
∴
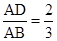，∵DE∥BC，
∴△ADE∽△ABC，
∴
，∴DE=
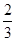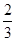×BC=×6=4，∵DE∥BC，
∴
，∴
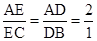，又∵EF∥AB，
∴
，∵AB=3，
∴EF=AB×
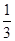=1，∵DE∥BC，EF∥AB，
∴四边形DBFE是平行四边形，
∴四边形DBFE的周长=2（DE+EF）=2（4+1）=10．
故答案为：10．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
