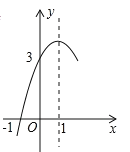题目内容
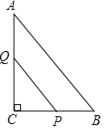
【题目】某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处回合，如图所示，以水平方向为
轴，喷水池中心为原点建立平面直角坐标系.
（1）求水柱所在抛物线（第一象限部分）的函数表达式；
（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？
【答案】（1）
；（2）王师傅必须在7米以内.
【解析】
（1）由抛物线的顶点坐标为（3，5），设抛物线解析式为y=a(x-3)+5，把（8，0）单人宽求出a的值，即可得抛物线解析式；（2）把y=1.8代入解析式求出x的值，根据函数图像的对称性求出负半轴的坐标即可.
（1）设
，过点
∴代入，解得
∴抛物线（第一象限部分）的函数表达式为
（2）
∴
或-1
，图象对称
负半轴为-7
答：王师傅必须在7米以内.
练习册系列答案
相关题目
【题目】某商店出售一款商品，经市场调查反映，该商品的日销售量y（件）与销售单价x（元）之间满足一次函数关系，关于该商品的销售单价，日销售量，日销售利润的部分对应数据如表：[注：日销售利润＝日销售量×（销售单价﹣成本单价）
销售单价x（元） | 75 | 78 | 82 |
日销售量y（件） | 150 | 120 | 80 |
日销售利润w（元） | 5250 | a | 3360 |
（1）根据以上信息，填空：该产品的成本单价是 元，表中a的值是 ，y关于x的函数关系式是 ；
（2）求该商品日销售利润的最大值．
（3）由于某种原因，该商品进价降低了m元/件（m＞0），该商店在今后的销售中，商店规定该商品的销售单价不低于68元，日销售量与销售单价仍然满足（1）中的函数关系，若日销售最大利润是6600元，直接写出m的值．
