题目内容
如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E.
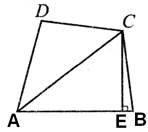
(1)若∠ADC+∠ABC=180°,求证:AD+AB =2AE;
(2)若AD+AB =2AE,求证:CD=CB.

(1)若∠ADC+∠ABC=180°,求证:AD+AB =2AE;
(2)若AD+AB =2AE,求证:CD=CB.
(1)可求证∠ADC=∠CBM.因此,△ADC≌△MBC,AD=BM.故AM="2AE=AB+" BM=AB+AD.
(2)可求证△ADC≌△MBC.所以,CD=CB
(2)可求证△ADC≌△MBC.所以,CD=CB
试题分析:(1)如图.延长AB到点M,使AE=ME.又CE⊥AB,
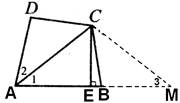
故△ACM为等腰三角形.因此,AC=CM,∠l=∠3.
已知∠1 =∠2,所以,∠3=∠L2.又∠ADC+∠ABC=180°,
于是,∠ADC=∠CBM.因此,△ADC≌△MBC,AD=BM.
故AM="2AE=AB+" BM=AB+AD.
(2)如图,延长AB到点M,使BM=AD.由2AE=AB+AD=AB+BM=AM,故AE=ME.
∵CE⊥AM,同(1)得AC=MC,∠2=∠3. ∵BM=AD,∴△ADC≌△MBC.从而,CD=CB.
点评:本题难度中等,主要考查学生对等腰梯形及全等三角形性质知识点的掌握与综合运用能力,为中考常考题型,要求学生牢固掌握解题技巧。

练习册系列答案
相关题目
 ,求这个多边形每一个内角的度数和它的边数.
,求这个多边形每一个内角的度数和它的边数.
 ,则添加下列一个条件后,仍无法判定
,则添加下列一个条件后,仍无法判定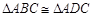 的是( )
的是( )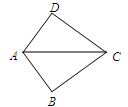
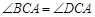
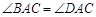
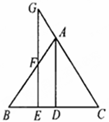
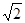 ,则此三角形移动的距离A A'是( )
,则此三角形移动的距离A A'是( )
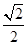
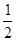

 AD⊥BC于D,EG⊥BC于G,(已知)
AD⊥BC于D,EG⊥BC于G,(已知) ∠ADC=∠EGC=90°,( )
∠ADC=∠EGC=90°,( )