题目内容
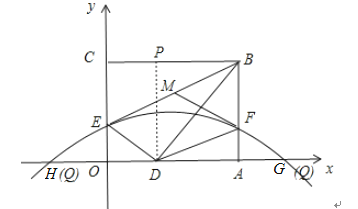
【题目】如图，折叠矩形OABC的一边BC，使点C落在OA边的点D处，已知折痕BE=
，且
=
，以O为原点，OA所在的直线为x轴建立如图所示的平面直角坐标系，抛物线l：y=
x2+
x+c经过点E，且与AB边相交于点F．
（1）求证：△ABD∽△ODE;
（2）若M是BE的中点，连接MF，求证：MF⊥BD；
（3）P是线段BC上一点，点Q在抛物线l上，且始终满足PD⊥DQ，在点P运动过程中，能否使得PD=DQ？若能，求出所有符合条件的Q点坐标；若不能，请说明理由．
【答案】
（1）
【解答】证明：
∵四边形ABCO为矩形，且由折叠的性质可知△BCE≌△BDE，
∴∠BDE=∠BCE=90°，
∵∠BAD=90°，
∴∠EDO+∠BDA=∠BDA+∠DAB=90°，
∴∠EDO=∠DBA，且∠EOD=∠BAD=90°，
∴△ABD∽△ODE；
（2）
【解答】
证明：
∵
=
，
∴设OD=4x，OE=3x，则DE=5x，
∴CE=DE=5x，
∴AB=OC=CE+OE=8x，
又∵△ABD∽△ODE，
∴
=
=
，
∴DA=6x，
∴BC=OA=10x，
在Rt△BCE中，由勾股定理可得BE2=BC2+CE2，即（
）2=（10x）2+（5x）2，解得x=1，
∴OE=3，OD=4，DA=6，AB=8，OA=10，
∴抛物线解析式为y=
x2+
x+3，
当x=10时，代入可得y=
，
∴AF=，BF=AB﹣AF=8﹣=
，
在Rt△AFD中，由勾股定理可得DF=
=
=，
∴BF=DF，
又M为Rt△BDE斜边上的中点，
∴MD=MB，
∴MF为线段BD的垂直平分线，
∴MF⊥BD；
（3）
【解答】
解：由（2）可知抛物线解析式为y=x2+x+3，设抛物线与x轴的两个交点为H、G，
令y=0，可得0=x2+x+3，解得x=﹣4或x=12，
∴H（﹣4，0），G（12，0），
①当PD⊥x轴时，由于PD=8，DM=DN=8，
故点Q的坐标为（﹣4，0）或（12，0）时，△PDQ是以P为直角顶点的等腰直角三角形；
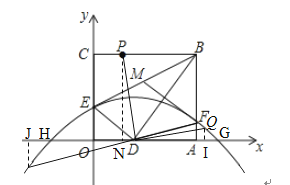
②当PD不垂直与x轴时，分别过P，Q作x轴的垂线，垂足分别为N，I，则Q不与G重合，从而I不与G重合，即DI≠8．
∵PD⊥DQ，
∴∠QDI=90°﹣∠PDN=∠DPN，
∴Rt△PDN∽Rt△DQI，
∵PN=8，
∴PN≠DI，
∴Rt△PDN与Rt△DQI不全等，
∴PD≠DQ，另一侧同理PD≠DQ．
综合①，②所有满足题设条件的点Q的坐标为（﹣4，0）或
（12，0）．
【解析】（1）由折叠和矩形的性质可知∠EDB=∠BCE=90°，可证得∠EDO=∠DBA，可证明△ABD∽△ODE；
（2）由条件可求得OD、OE的长，可求得抛物线解析式，结合（1）由相似三角形的性质可求得DA、AB，可求得F点坐标，可得到BF=DF，又由直角三角形的性质可得MD=MB，可证得MF为线段BD的垂直平分线，可证得结论；
（3）过D作x轴的垂线交BC于点G，设抛物线与x轴的两个交点分别为M、N，可求得DM=DN=DG，可知点M、N为满足条件的点Q，可求得Q点坐标．
