题目内容
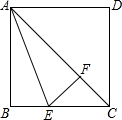 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
(1)图中与线段BE相等的所有线段是________;选择图中与BE相等的任意一条线段,并加以证明;
(2)若BE=1,求△AEC的面积.
(1)图中与线段BE相等的所有线段是EF和CF,
证明:∵四边形ABCD是正方形,
∴∠B=90°,∠ACB= ∠DCB=45°,
∠DCB=45°,
∵AE平分∠BAC,EF⊥AC,
∴BE=EF,
∵EF⊥AC,
∴∠EFC=90°,
∵∠ACB=45°,
∴∠FEC=45°=∠FCE,
∴EF=FC=BE,
故答案为:EF、CF;
(2)解:∵在Rt△EFC中,BE=EF=CF=1,由勾股定理得:CE=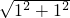 =
= ,
,
∴BC=1+ =AB,
=AB,
在Rt△ABC中,由勾股定理得:AC=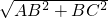 =2+
=2+ ,
,
∴△ACE的面积是 ×AC×EF=
×AC×EF= ×(2+
×(2+ )×1=1+
)×1=1+
 .
.
分析:(1)BECF,理由是根据正方形性质得出∠B=90°,∠ACB=45°,根据角平分线性质求出EF=BE,求出∠FEC=∠FCE=45°,推出EF=CF,即可得出答案;
(2)根据勾股定理求出CE,得出BC和AB的值,再根据勾股定理求出AC,根据三角形的面积公式求出即可.
点评:本题考查的知识点有正方形性质、勾股定理、等腰三角形的性质和判定、角平分线性质,能综合运用性质进行推理和计算是解此题的关键,题目具有一定的代表性,是一道比较好的题目.
证明:∵四边形ABCD是正方形,
∴∠B=90°,∠ACB=
 ∠DCB=45°,
∠DCB=45°,∵AE平分∠BAC,EF⊥AC,
∴BE=EF,
∵EF⊥AC,
∴∠EFC=90°,
∵∠ACB=45°,
∴∠FEC=45°=∠FCE,
∴EF=FC=BE,
故答案为:EF、CF;
(2)解:∵在Rt△EFC中,BE=EF=CF=1,由勾股定理得:CE=
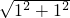 =
= ,
,∴BC=1+
 =AB,
=AB,在Rt△ABC中,由勾股定理得:AC=
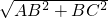 =2+
=2+ ,
,∴△ACE的面积是
 ×AC×EF=
×AC×EF= ×(2+
×(2+ )×1=1+
)×1=1+
 .
.分析:(1)BECF,理由是根据正方形性质得出∠B=90°,∠ACB=45°,根据角平分线性质求出EF=BE,求出∠FEC=∠FCE=45°,推出EF=CF,即可得出答案;
(2)根据勾股定理求出CE,得出BC和AB的值,再根据勾股定理求出AC,根据三角形的面积公式求出即可.
点评:本题考查的知识点有正方形性质、勾股定理、等腰三角形的性质和判定、角平分线性质,能综合运用性质进行推理和计算是解此题的关键,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
相关题目
 .
.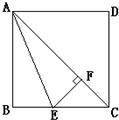 14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.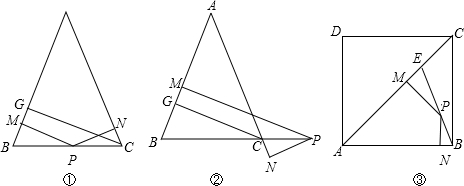
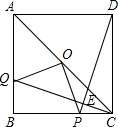 点P,连接OP,OQ;
点P,连接OP,OQ;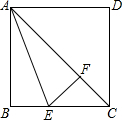 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.