题目内容
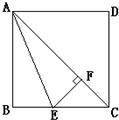 14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
14、如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.(1)图中与线段BE相等的所有线段是
EF和FC
;(2)选择图中与BE相等的任意一条线段,并加以证明.
分析:△ABE与△AFE可看作关于直线AE的轴对称,寻找它们全等的条件,从而得出BE=EF,再证明△EFC为等腰直角三角形,从而得出EF=FC.
解答:解:(1)EF和FC;
∵AE平分∠BAC,EF⊥AC交AC于点F,BE⊥AB,
∴BE=EF;
又∵AC是正方形ABCD的对角线,
∴∠ECF=45°,
∴∠CEF=45°,
∴EF=FC.
(2)证明:∵四边形ABCD是正方形,
∴∠B=90°,
又∵EF=AC,
∴∠AFE=∠B,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
又∵AE=AE,
∴△ABE≌△AFE(AAS),
∴BE=EF.
∵AE平分∠BAC,EF⊥AC交AC于点F,BE⊥AB,
∴BE=EF;
又∵AC是正方形ABCD的对角线,
∴∠ECF=45°,
∴∠CEF=45°,
∴EF=FC.
(2)证明:∵四边形ABCD是正方形,
∴∠B=90°,
又∵EF=AC,
∴∠AFE=∠B,
∵AE平分∠BAC,
∴∠BAE=∠FAE,
又∵AE=AE,
∴△ABE≌△AFE(AAS),
∴BE=EF.
点评:解答本题要充分里利用正方形的特殊性质,角平分线的性质,注意在正方形中的特殊三角形的应用.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 .
.
 点P,连接OP,OQ;
点P,连接OP,OQ;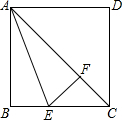 如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.
如图,AC是正方形ABCD的对角线,AE平分∠BAC,EF⊥AC交AC于点F.