题目内容
如图①,已知△ABC中,AB=AC,点P是BC上的一点,PN⊥AC于点N,PM⊥AB于点M,CG⊥AB于点G点.(1)则CG、PM、PN三者之间的数量关系是
(2)如图②,若点P在BC的延长线上,则PM、PN、CG三者是否还有上述关系,若有,请说明理由,若没有,猜想三者之间又有怎样的关系,并证明你的猜想;
(3)如图③,AC是正方形ABCD的对角线,AE=AB,点P是BE上任一点,PN⊥AB于点N,PM⊥AC于点M,猜想PM、PN、AC有什么关系;(直接写出结论)

分析:(1)过P作PH垂直CG于H,可通过证明△PNC≌△PHC得出CG=GH+HC=PM+PN.
(2)过C作CH垂直MP于H,可通过证明△PNC≌△PHC得出PM=CG+PN.
(3)令点P和点B重合可轻易得出猜想.
(2)过C作CH垂直MP于H,可通过证明△PNC≌△PHC得出PM=CG+PN.
(3)令点P和点B重合可轻易得出猜想.
解答: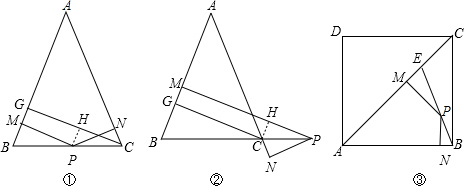
解:(1)方法一:过P作PH垂直CG于H,
∵PM⊥AB,CG⊥AB,
∴∠AMP=∠MGH=∠PHG=90°,
∴四边形MPHG是矩形,
∴PM=GH,PH∥AB,
∴∠HPC=∠B,
∵AB=AC,
∴∠B=∠ACB,
∴∠HPC=∠NCP,
又∵PH⊥CG,PN⊥AC,
∴∠PHC=∠CNP=90°,
∴△PHC≌△CNP,
∴CH=PN,
∴CG=GH+HC=PM+PN.
方法二:PM+PN=CG.
连接AP,则△ABC被分成△APB与△APC,
则△ABC的面积=△APB的面积+△APC的面积,
即
×AC×CG=
×AB×PM+
×AC×PN,
∵AB=AC,
∴PM+PN=CG;
(2)过C作CH垂直MP于H,
∠HPC+∠ABC=90°∠NPC+∠PCN=90
∵∠ABC=∠ACB=∠PCN
∴∠HPC=∠NPC
又PH⊥CG,PN⊥AC
∴△PNC≌△PHC?PM=CG+PN.
(3)猜想PM+PN=
AC(令点P与点B重合)

解:(1)方法一:过P作PH垂直CG于H,
∵PM⊥AB,CG⊥AB,
∴∠AMP=∠MGH=∠PHG=90°,
∴四边形MPHG是矩形,
∴PM=GH,PH∥AB,
∴∠HPC=∠B,
∵AB=AC,
∴∠B=∠ACB,
∴∠HPC=∠NCP,
又∵PH⊥CG,PN⊥AC,
∴∠PHC=∠CNP=90°,
∴△PHC≌△CNP,
∴CH=PN,
∴CG=GH+HC=PM+PN.
方法二:PM+PN=CG.
连接AP,则△ABC被分成△APB与△APC,
则△ABC的面积=△APB的面积+△APC的面积,
即
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=AC,
∴PM+PN=CG;
(2)过C作CH垂直MP于H,
∠HPC+∠ABC=90°∠NPC+∠PCN=90
∵∠ABC=∠ACB=∠PCN
∴∠HPC=∠NPC
又PH⊥CG,PN⊥AC
∴△PNC≌△PHC?PM=CG+PN.
(3)猜想PM+PN=
| 1 |
| 2 |
点评:本题主要考查通过全等三角形转化线段从而得出线段之间的关系,在第三问中关键在于选取点P的位置与点B重合,可很容易的得出正确的猜想.

练习册系列答案
相关题目
 定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.
定义:若某个图形可分割为若干个都与他相似的图形,则称这个图形是自相似图形.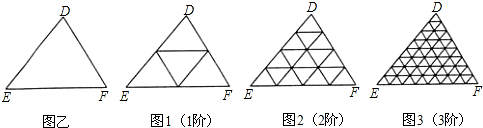
 如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=
如图,若已知△ABC中,D、E分别为AB、AC的中点,则可得DE∥BC,且DE=

